Variational Diffusion Models
- Variational Diffusion Models, Kingma et al., 2021, arXiv:2107.00630
- Keyword: DDPM, Variational Lower Bounds
- Problem: Unstable noise scheduling, finite step diffusion process.
- Solution: Continuous-time diffusion process, joint training of noise scheduler.
- Benefits: Improved theoretical model understanding, faster optimization, better perceptual quality.
- Contribution: Simplifying model expression with variational lower bounds in terms of SNR.
Introduction
최근 Diffusion 모델은 이미지, 오디오 등 생성 분야에서 높은 perceptual quality를 보인다. [Ho et al., 2020]의 DDPM과 [Kong et al., 2020, Chen et al., 2020]의 DiffWave, WaveGrad의 경우, 일전 포스트에서 다룬 적이 있다. [post]
Variational Diffusion Models, 이하 VDM에서는 이에 더 나아가 signal-to-noise ratio와 variational lower bounds를 통한 formulation의 단순화, infinite steps를 상정한 process의 유도와 noise scheduler의 joint training 가능성에 관한 이야기를 나눈다.
Diffusion Models
생성 모델의 가장 중요한 concept는 dataset과 관측치 $x$가 있을 때, marginal distribution $p(x)$를 추정하는 것이다. Diffusion 모델은 latent variable model로 latent의 hierarchy를 상정하고, variational lower bounds, 이하 VLB를 통해 marginal loglikelihood의 lower-bound를 maximize 하는 학습 방식을 취한다. 이러한 프로세스는 [Nielsen et al., 2020.]의 SurVAE Flows [post]에서 Stochastic transform을 활용한 flow의 일종으로 일반화되기도 한다.

Figure 2: The directed graphical model considered in this work. (Ho et al., 2020)
기존까지의 Diffusion 모델은 finite step의 markov chain을 가정하며, 매 transition 마다 noise를 더해가는 방식을 취한다. latent sequence $z_t$가 있다면, t=0 부터 t=1까지의 forward-time diffusion process를 정의할 수 있다.
$$q(z_t|x) = \mathcal N(\alpha_t x, \sigma_t^2 \mathrm{I})$$
이때 $\alpha_t,\ \sigma_t^2: [0, 1] \to \mathbb R^+$의 실수 함수는 smooth하여 정의역에서 미분이 유한함을 가정한다. 또한 $\alpha_t^2/\sigma_t^2$의 비율이 단조 감소하여, t가 증가함에 따라 noise의 비율이 커지도록 구성한다. 이에 t=0에서 데이터 $x$에 가까울 것이고, t=1에서 gaussian noise에 가까워질 것이다.
$0\le s \lt t \lt u \le 1$의 latent $z_s, z_t, z_u$와 joint distribution은 first-order Markov chain으로 가정하여 $q(z_u|z_t, z_s) = q(z_u|z_t)$를 상정한다. 이에 따른 conditional distribution은 다음과 같이 표기할 수 있다.
$$q(z_t|z_s) = \mathcal N(\alpha_{t|s}z_s, \sigma^2_{t|s}\mathrm I), \ \ \mathrm{where} \ \alpha_{t|s} = \alpha_t / \alpha_s \ \mathrm{and} \ \sigma^2_{t|s} = \sigma^2_t - \alpha^2_{t|s}\sigma^2_s$$
reverse time process의 경우에는 다음과 같다.
$$q(z_s|z_t, x) = \mathcal N(\mu_Q(z_t, x; s, t), \sigma^2_{Q, s, t}\mathrm I) \ \ \mathrm{with} \ \sigma^2_{Q, s, t} = \sigma^2_{t|s}\sigma^2_s/\sigma^2_t \\ \mathrm{and} \ \ \mu_Q(z_t, x; s, t) = \frac{1}{\alpha_{t|s}}(z_t + \sigma^2_{t|s}\nabla_{z_t}\log q(z_t|x)) = \frac{\alpha_{t|s}\sigma^2_s}{\sigma_t^2}z_t + \frac{\alpha_s\sigma^2_{t|s}}{\sigma_t^2}x$$
Reverse time process as Generative model
Diffusion model은 reverse time process를 근사하는 방식의 생성 모델이며, 위 formulation에서 data 부분을 denoising model $\hat x_\theta(z_t, t)$로 대체하게 된다.
$$p(z_s|z_t) = q(z_s|z_t, x = \hat x_\theta(z_t; t)) = \mathcal N(z_s; \mu_\theta(z_t; s, t), \sigma^2_{Q, s, t}\mathrm{I})$$
이에 따라 네트워크는 $\mu_\theta(z_t; s, t) \approx \mu_Q(z_t, x; s, t)$의 근사를 목표로 하게 된다.
$$\mu_\theta(z_t; s, t) = \frac{\alpha_{t|s}\sigma^2_s}{\sigma^2_t}z_t + \frac{\alpha_s\sigma^2_{t|s}}{\sigma^2_t}\hat x_\theta(z_t; t) = \frac{1}{\alpha_{t|s}}z_t - \frac{\sigma^2_{t|s}}{\alpha_{t|s}\sigma_t}\hat\epsilon_\theta(z_t; t) = \frac{1}{\alpha_{t|s}}z_t + \frac{\sigma^2_{t|s}}{\alpha_{t|s}}s_\theta(z_t; t)$$
이는 model의 관점에 따라 3가지의 해석이 가능하다.
- $z_t$의 noised data로부터 원본을 복원하는 denoising model $\hat x_\theta(z_t; t)$
- $z_t$에 포함된 noise를 추정하는 noise estimation model $\epsilon_\theta(z_t; t) = (z_t - \alpha_t\hat x_\theta(z_t; t)) / \sigma_t$
- gradient를 추정하는 score matching model $s_\theta(z_t; t) = (\alpha_t \hat x_\theta(z_t; t) - z_t)\sigma^2_t$
3번의 경우 optimal model이 실제 scores를 추정하여, $s^*(z_t; t) = \nabla_z\log q(z_t)$, reverse time process의 최초 formulation과 일치해진다.
VDM은 DDPM에서 제안한 noise estimation objective를 취할 것이고, 편의상 formulation은 denoising model을 상정할 것이다.
Relation between prior works
기존의 Diffusion model은 기본적으로 finite step T를 상정하므로, 위 formulation에서 segment size $\tau = 1 / T$를 잡고, [0, 1]의 범위를 T개의 segment로 discretize한 형태로 볼 수 있다. 다음은 diffusion 모델에서 상정하는 marginal likelihood이다.
$$p(x) = \int_z p(x|z_0)\left(\prod^T_{i=1}p(z_{s(i)}|z_{t(i)})\right)p(z_1) \\ \mathrm{where} \ \ s(i) = (i - 1) / T, \ t(i) = i / T$$
각각의 diffusion 모델은 $\alpha_t, \sigma_t$를 적절히 구성하여 $q(z_1|x) \approx \mathcal N(z_1; 0, \mathrm{I})$의 standard gaussian과 근사히 둔다. 마찬가지로 initial latent와 데이터의 reconstruction을 위해 $\sigma_0$ 대비 $\alpha_0$의 크기를 키움으로써 true distribution에 가깝게 근사하도록 구성한다.
Signal-to-noise ratio
위의 가정에서 중요한 점은 [$\sigma_t$ 대비 $\alpha_t$의 비율]을 적절히 가정함으로써 $p(z_1)$은 standard gaussian에, $p(z_0)$는 data distribution에 근사하고자 한다는 점이다.
이때 $z_t = \alpha_t x + \sigma_t\epsilon$에서 $\alpha_t$는 실제 신호의 비, $\sigma_t$는 noise의 비로, [$\sigma_t$ 대비 $\alpha_t$의 비율]은 신호 대 잡음의 비율이라 볼 수 있고, 이를 SNR, signal-to-noise ratio라고 한다.
$$\mathrm{SNR}(t) = \alpha_t^2/\sigma^2_t$$
이 중 DDPM에서는 $\alpha_t = \sqrt{1 - \sigma^2_t}$를 상정하여 variance-preserving diffusion process를 가정한다. 일부 모델에서는 $\alpha_t=1$의 상수로 잡고 $\sigma_t$를 늘리는 variance-exploding diffusion process를 상정하기도 한다. 이는 SNR(t)로도 재작성될 수 있다.
$$\alpha^2_t = \mathrm{SNR}(t) / (1 + \mathrm{SNR}(t)), \ \ \sigma^2_t = 1 / (1 + \mathrm{SNR}(t))$$
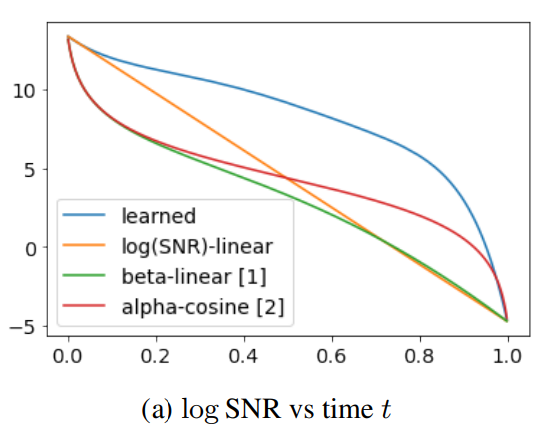
일전의 가정에 따라 diffusion 모델에서 SNR 함수는 단조 감소 함수가 된다. 기존까지 모델에서는 이 SNR 함수가 well-engineered 함수로 가정되었다면, VDM에서는 SNR을 trainable한 component로 가정할 것이다.
Variational Lower Bounds
DDPM에서는 VLB를 통해 diffusion process로부터 KL-divergence 기반의 objective를 구성한다. 이때 $\mathcal L_T(x)$는 diffusion loss이다.
$$-\log p(x) \le D_\mathrm{KL}(q(z_1|x)||p(z_1)) + \mathrm E_{q(z_0|x)}[-\log p(x|z_0)] + \mathcal L_T(x) \\ \mathcal L_T(x) = \sum^T_{i=1}\mathbb E_{q(z_{t(i)}|x)}D_\mathrm{KL}[q(z_{s(i)}|z_{t(i)}, x)||p(z_{s(i)}|z_{t(i)})]$$
그리고 이는 DDPM에서 weighted noise estimation loss의 형태로 reparametrized된다.
$$\mathcal L_{\mathrm{simple}}(x) = \mathbb E_{\epsilon\sim p(\epsilon)}[||\epsilon - \hat\epsilon_\theta(\alpha_t x + \sigma_t \epsilon; t)||_2^2]$$
VDM에서는 denoising model을 formulation으로 활용한다.
$$\mathcal L_T(x) = \frac{1}{2}\mathbb E_{\epsilon \sim \mathcal N(0, \mathrm{I}), i \sim U\{1, T\}}\left[\frac{(\mathrm{SNR}(s) - \mathrm{SNR}(t))}{1/T}||x - \hat x_\theta(z_t; t)||^2_2\right]$$
Variational Diffusion Models
VDM의 contribution은 다음과 같다.
- $T \to \infty$를 상정하여 continuous-time loss를 유도한다.
- noise scheduler에 continuous-time loss가 invariant 함을 보인다.
- noise scheduler를 학습 가능한 네트워크로 구성하고, objective를 제안한다.
- Fourier feature를 통해 finer-scale에서의 perceptual quality를 높였다.
아래에서는 이에 대해 하나씩 풀어본다.
Why continuous time
이전 실험들에서는 diffusion steps가 많아질수록 학습이 안정화되고 perceptual quality가 높아짐을 실험적으로 확인할 수 있었다.
$$\mathcal L_{2T}(x) - \mathcal L_T(x) = \mathbb E_{t, \epsilon}\left[c(t’)(||x - \hat x _\theta(z _{t’}; t’)||^2_2 - ||x - \hat x _\theta(z_t; t)||^2_2) \right] \\ \mathrm{where} \ \ t’ = t - \frac{1}{2T}, \ \ c(t) = \mathrm{SNR}(t’ - \frac{1}{2T}) - \mathrm{SNR}(t’)$$
diffusion step이 다른 두 loss를 빼게 되면, $t’ < t$이므로 $z_{t’}$이 상대적으로 원본에 가까운 latent이고, $\hat x_\theta$가 충분히 학습된 모델이라면 원본 복원이 쉬운 latent 쪽의 loss가 작게 구성될 것이다.
따라서 거의 항상 $\mathcal L_{2T}(x) - \mathcal L_T(x) < 0$을 상정할 수 있고, diffusion steps가 늘어날수록 VLB를 통해 더 높은 likelihood lower-bounds를 추정할 수 있게 된다.
VDM에서는 $T\to\infty$의 극한을 취해 VLB의 하한을 높이고자 한다. 이렇게 되면 segment size $\tau = 1 / T$는 0에 가까워지고, continuous time에 대한 loss로 취급할 수 있다. 그리고 실제로 이러한 concept가 perceptual quality의 향상에도 영향을 끼쳤음을 보였다.
Continuous-time loss
$T\to\infty$와 $\tau = 1 / T\to 0$를 상정한다면, $\mathcal L_\infty(x)$는 다음으로 유도할 수 있다.
$$\begin{align*} \lim_{T\to\infty}\mathcal L_T(x) &= \lim_{T\to\infty}\frac{1}{2}\mathbb E_{\epsilon\sim\mathcal N(0, \mathrm{I}), i\sim U\{1, T\}}\left[\frac{(\mathrm{SNR}(s) - \mathrm{SNR}(t))}{1/T}||(x - \hat x_\theta(z_t; t)||^2_2\right]\\ &= \lim_{T\to\infty}\frac{1}{2}\mathbb E_{\epsilon\sim\mathcal N(0, \mathrm{I}), i\sim U\{1, T\}}\left[\frac{\mathrm{SNR}(t - \tau) - \mathrm{SNR}(t)}{\tau}||x - \hat x_\theta(z_t; t)||^2_2\right] \\ &= -\frac{1}{2}\mathbb E_{\epsilon\sim\mathcal N(0, \mathrm{I}), t\sim\mathcal U(0, 1)}\left[\frac{d\mathrm{SNR}(t)}{dt}||x - \hat x_\theta(z_t; t)||^2_2\right] \end{align*}$$
epsilon estimation의 관점에서는 다음과 같이 쓸 수 있다.
$$\mathcal L_\infty(x) = -\frac{1}{2}\mathbb E_{\epsilon\sim\mathcal N(0, \mathrm{I}), t\sim\mathcal U(0, 1)}\left[\log\mathrm{SNR’}(t)||\epsilon - \hat\epsilon_\theta(z_t; t)||^2_2\right]$$
이 때 $\log\mathrm{SNR}’(t) = d\log[\mathrm{SNR}(t)]/dt = \mathrm{SNR}’(t)/\mathrm{SNR}(t)$이다.
Invariance to the noise schedule in continuous time
VDM은 continuous-time loss의 변수 t를 $v = \mathrm{SNR}(t)$의 snr변수로 reparametrize하여 관찰한다. SNR이 단조 감수이므로 $dv = \mathrm{SNR}’(t)dt$에 따라 치환하면 다음과 같다.
$$\begin{align*}
\mathcal L_\infty(x)
&= -\frac{1}{2}\mathbb E_{\epsilon\sim\mathcal N(0, \mathrm{I}), t\sim\mathcal U(0, 1)}\left[\mathrm{SNR}’(t)||x - \hat x_\theta(z_t; t)||^2_2\right] \\
&= -\frac{1}{2}\mathbb E_{\epsilon \sim\mathcal N(0, \mathrm{I})}\int_0^1 \mathrm{SNR}’(t)||x - \hat x_\theta(z_t; t)||^2_2dt \\
&= \frac{1}{2}\mathbb E_{\epsilon\sim\mathcal N(0, \mathrm{I})}\int_\mathrm{SNR_{min}}^\mathrm{SNR_{max}}||x - \hat x_\theta(z_v, v)||_2^2dv \\
\mathrm{where} \
&\mathrm{SNR _{min}} = \mathrm{SNR}(1), \mathrm{SNR _{max}} = \mathrm{SNR}(0) \\
&z_v = z _{\mathrm{SNR}^{-1}(v)}, \hat x _\theta(z, v) = \hat x _\theta(z, \mathrm{SNR}^{-1}(v))
\end{align*}
$$
이 식에서 중요한 점은 $\mathcal L_\infty$를 결정하는 요소가 양단점인 $\mathrm{SNR_{min}}$과 $\mathrm{SNR_{max}}$ 뿐이란 것이고, SNR 함수가 어떻게 생겼는지와는 무관하다는 점이다. 즉 SNR의 양단이 같은 두 continuous-time loss는 equivalence임을 알 수 있다.
또한 $v = \alpha^2_v / \sigma^2_v$에 따라 $\sigma_v = \alpha_v / \sqrt v$로 정리할 수 있고, $z_v = \alpha_v x + \sigma_v \epsilon = \alpha_v(x + \epsilon / \sqrt v)$로 고정된 v에 대해 $\alpha$와 $\sigma$의 변인을 축약할 수 있다. 이는 서로 다른 variance policy에 대해 rescale 관계로 표현할 수 있다는 점이고, $z^A_v = (\alpha^A_v / \alpha^B_v)z^B_v$, 이에 따라 $\hat x^B_\theta(z^B_v, v) = \hat x^A_\theta((\alpha^A_v/\alpha^B_v)z^B_v, v)$의 model equivalence도 구성할 수 있다.
Weighted continuous-time loss
DDPM에서는 이를 noise estimation loss의 형태로 바꾸면서 reweighting을 진행했고, 이는 continuous-time loss에서도 적용할 수 있다.
$$\mathcal L_\infty(x, w) = \frac{1}{2}\mathbb E_{\epsilon \sim \mathcal N(0, \mathrm{I})}\int^\mathrm{SNR_{max}}_\mathrm{SNR _{min}} w(v)||x - \hat x _\theta(z _v, v)||^2 _2dv$$
VLB는 아니지만 noisier data를 강조하는 등의 policy를 통해 실제 FID, IS 등 perceptual quality를 측정하는 metric에서 때에 따라 성과를 보이기도 한다.
Monte-carlo estimation
하지만 실상 적분을 하는 것은 intractable 하기 때문에 샘플링을 통한 estimation이 필요하다. 이에 VLB objective를 단순화하고, sampling과 batch stats를 활용한 monte-carlo estimation을 시행한다.
$$\mathcal L^{MC}_\infty(x, w, \gamma) = \frac{1}{2}\gamma’(t)w(\gamma(t))||\epsilon - \hat\epsilon _\theta(z_t; \gamma(t))||^2_2$$
이때 $\gamma$는 noise scheduler로 $\gamma(t) = -\log\mathrm{SNR}(t) = \log[\sigma^2_t/\alpha^2_t]$를 상정하고, $z_t = \alpha_t x + \sigma_t\epsilon$, $\epsilon \sim \mathcal N(0, \mathrm{I}), t \sim \mathcal U(0, 1)$의 샘플링을 진행한다. 여기서는 reweighting 함수는 $w(\cdot) = 1$의 상수 함수로 가정한다.
또한 VDM은 보다 효율적인 시간축 샘플링을 위해 최초 시점 $u_0 \sim \mathcal U(0, 1)$을 잡고, batch size k에 대해 $t_i = \mathrm{mod}(u_0 + i/k, 1)$의 선형 보간 방식을 취한다. 이렇게 하는 것이 [0, 1] 범주에서 더 uniform하게 분포한 시간점들을 샘플링 할 수 있고, 실제로 MC의 분산을 줄일 수 있었다고 한다.
Learning noise scheduler
기존까지의 모델들이 고정된 SNR 함수를 활용했다면, VDM은 파라미터 $\eta$를 통해 학습 가능한 SNR 함수 $\mathrm{SNR}(t) = \exp(-\gamma_\eta(t))$를 상정한다. 이는 SNR 함수가 단조 감소 함수이기 때문에 $\gamma_\eta(t) = -\log\mathrm{SNR}(t)$로 두어 단조 증가 함수의 꼴로 네트워크를 모델링 하기 위함이다.
실제로 VDM에서 제안하는 learnable noise scheduler는 다음과 같다.
# t: [B]
l1 = Linear(1, 1)(t)
l2 = Linear(1, 1024)(l1)
l3 = Linear(1024, 1)(sigmoid(l2))
v = l1 + l3
여기서 projection weight가 모두 양수라면 t가 0에서 1로 증가함에 따라 $\gamma_\eta(t) = -\log\mathrm{SNR}(t)$도 단조 증가 하는 것이 보장된다.
하지만 이렇게 학습된 noise scheduler는 실상 양단점을 제외하면 continuous-time loss에 영향을 미치지 않음을 앞서 보였다. 따라서 VDM은 noise scheduler 학습의 목적성을 다른 방향으로 잡는다.
VDM은 Monte-carlo estimation의 분산을 줄이는 objective를 통해 $\gamma$를 학습하며, $\mathbb E[\mathcal L^{MC} _\infty(x, w, \gamma)^2] = \mathcal L _\infty(x, w)^2 + \mathrm{Var}[\mathcal L^{MC} _\infty(x, w, \gamma)]$의 첫 번째 term $\mathcal L _\infty(x, w)^2$은 $\eta$와 무관하므로 loss 제곱을 줄이는 방향으로 학습한다.
$$\mathbb E[\nabla _\eta \mathcal L^{MC} _\infty(x, w, \gamma _\eta)^2] = \nabla _\eta\mathrm{Var}[\mathcal L^{MC} _\infty(x, w, \gamma _\eta)]$$
이 경우 역전파를 두 번 해야 하는 문제가 있으며, 이를 효율적으로 처리하기 위해 $\gamma$ 함수 이전에 역전파 함수를 hooking하는 방식을 제안한다.
$$\frac{d}{d\eta}[\mathcal L^{MC}_\infty(x, \gamma _\eta)^2]=2\frac{d}{d\mathrm{SNR}}[\mathcal L^{MC} _\infty(x, \mathrm{SNR})]\odot\mathcal L^{MC} _\infty(x, \mathrm{SNR})\frac{d}{d\eta}[\mathrm{SNR}(\eta)]$$
앞선 식에서 $2\mathcal L^{MC} _\infty(x, \mathrm{SNR})$를 제외하면 기존의 역전파 방식과 일치하므로, hooking을 통해 gradient에 loss를 곱하는 방식이다. 이 경우 불필요한 연산을 줄일 수 있다.
이런 식으로 분산을 조절하는 방식은 실제로 학습 속도를 높이는데 도움을 주었다고 한다.
Fourier features
VDM에서는 finer detail을 위해 fourier feature를 denoising model의 입력에 concat하여 넘겼다. 실제로 이 접근은 high frequency detail에 도움을 주었다고 한다. $n\in\{7, 8\}$일 때 다음을 상정한다.
$$f^n_{i, j, k} = \sin(z_{i, j, k}2^n\pi), \ \ g^n_{i, j, k} = \cos(z_{i, j, k}2^n\pi)$$
Experiments
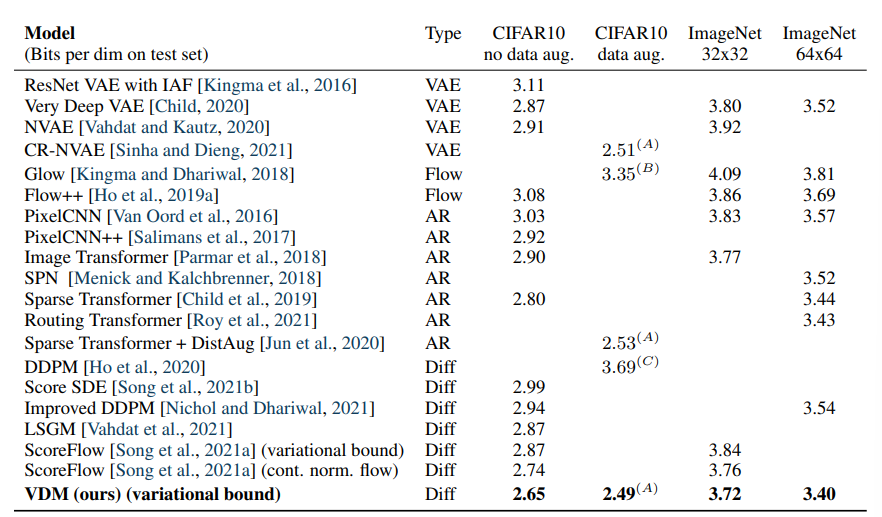
Table 1: Summary of our findings for density modeling tasks. (Kingma et al., 2021)
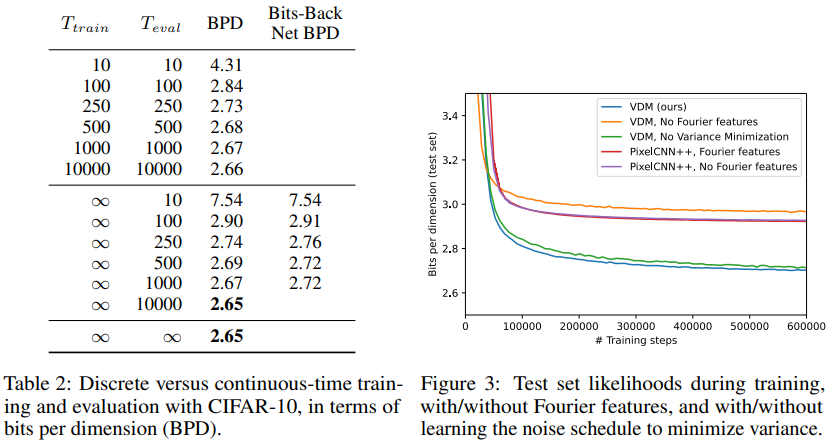
다음은 T에 따른 BPD이다. 실제로 train과 eval의 샘플링 수 모두에서 T가 증가할 수록 BPD가 줄어드는 것을 확인할 수 있었다.
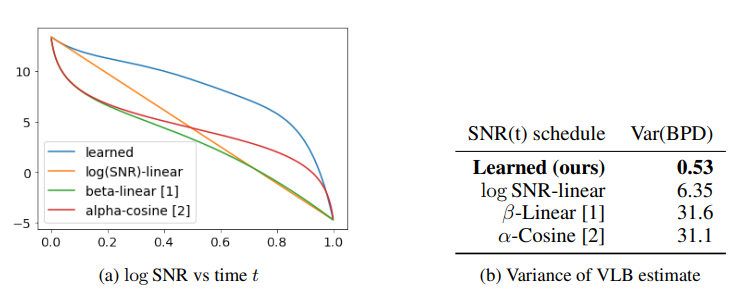
Figure 4: Our learned continuous-time variance-minimizing noise schedule SNR(t) for CIFAR-10, (Kingma et al., 2021)
Discussion
Contribution과 글의 전개가 무척 깔끔했다. Diffusion의 소개와 formulation 방식에 따른 해석 가능성을 정리하고, 품질 향상을 위한 지점으로 유한한 timestep을 상정, continuous-time으로 확장과 MCMC의 안정성 확보를 위한 learnable noise scheduler까지 문단 문단이 꽉 찬 느낌이었다.
VDM을 활용해 DiffWave를 개선한 코드를 개인적으로 작성해 보았다. 아직 결과가 나오기엔 시간이 필요하지만, 좋은 결과를 기대하고 있다.
- revsic/jax-variational-diffwave: Jax/Flax implementaton of Variational-DiffWave.
Reference
[1] Ho, J., Jain, A. and Abbeel, P. Denoising Diffusion Probabilistic Models. In NeurIPS 2020.
[2] Kong, Z., Ping, W., Zhao, K. and Catanzaro, B. DiffWave: A Versatile Diffusion Model for Audio Synthesis. In ICLR 2021.
[3] Chen, N., Zhang, Y., Zen, H., Weiss, R. J., Norouzi, M. and Chan, W. WaveGrad: Estimating Gradients for Waveform Generation.
[4] Kingma, D. P., Salimans, T., Poole, B. and Ho, J. Variational Diffusion Models.