SurVAE Flows
- SurVAE Flows: Surjections to Bridge the Gap between VAEs and Flows, Nielsen et al. In NeuRIPS 2020, arXiv.
- Keyword: Bayesian, Normalizing Flow, SurVAE Flows
- Problem: Specialized network architectures of normalizing flows
- Solution: Unifying several probabilistic models with surjections
- Benefits: Modulized, composable framework for probabilistic models
- Weakness or Future work: -
Series: Normalizing flow
- Normalizing flow, Real NVP [link]
- Glow, Flow++ [link]
- ANF, VFlow [link]
- i-ResNet, CIF [link]
- SurVAE Flows [this]
Normalizing Flows
Normalizing flow, 이하 NF는 differentiable bijective를 활용하여 expressive한 확률 모델을 구성하는데 기여해 왔다. NF는 1) forward 2) inverse 3) likelihood의 크게 3가지 interface를 통해 composable 하고 modular 한 형태로 구성되며, Rezende and Mohamed, 2015[1]를 시작으로 꾸준히 발전해 왔다.
이 과정에서 NF의 여러 가지 문제가 발견되었고, 그중 대표적으로 dimensionality problem은 ANF[5], VFlow[6]에서 augmentation을 도입하며 해결, misspecified prior의 문제는 CIF[7]에서 continuous index를 도입함으로써 해결하고자 했다.
그 외의 확률 모델로는 VAE와 GAN 정도가 대표적이며, VAE의 경우에는 ANF[5]에서 일반화하고자 하는 시도가 있었다.
이번에 소개하고자 하는 논문은 여러 확률 모델을 unifying 할 수 있는 composable하고 modular한 framework를 구성할 수 있는가에 대한 물음에서 시작한다. 그를 위해 저자들은 SurVAE Flows라는 framework를 제안하며, 여러 확률 모델을 unifying 하면서도 max pooling, absolute, sorting, stochastic permutation 등을 NF에 접목할 수 있게 구성하여, 더욱 expressive한 확률 모델 구성이 가능함을 보일 것이다.
Preliminaries
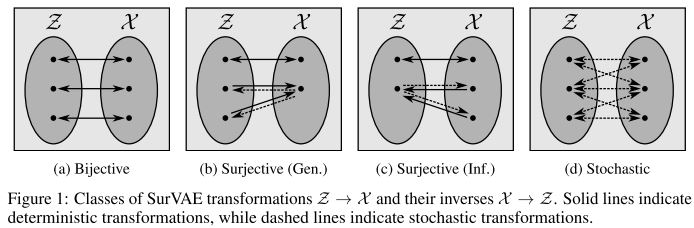
$x\in\mathcal X, \ z \in \mathcal Z$의 두 개 변수와 각각의 prior distribution $x \sim p(x), \ z \sim p(z)$을 상정한다. 이때 deterministic mapping $f: \mathcal Z \to \mathcal X$가 bijective이기 위해서는 surjective하고 injective 해야 한다.
- surjective: $\forall x \in \mathcal X, \exists z \in \mathcal Z: \ x = f(z)$
- injective: $\forall z_1, z_2 \in \mathcal Z, \ f(z_1) = f(z_2) \Rightarrow z_1 = z_2$
만약 mapping이 deterministic 하지 않다면, stochastic mapping이라 하고 $x \sim p(x|z)$로 표기한다.
NF는 기본적으로 bijective를 통한 change of variables $p(x) = p(z)|\det \nabla_x f^{-1}(x)|$를 근간으로 한다. VAE의 경우에는 stochastic transform을 차용하여 generative process $p(x) = p(z)p(x|z)$를 구성하고, variational posterior $z\sim q(z|x)$를 통해 likelihood의 lower bound $\mathbb E_{z\sim q(z|x)}\log [p(x, z)/q(z|x)]$ 를 추정한다.
Unifying Stochastic Transform
기본적으로 NF는 1) forward transform $f: \mathcal Z \to \mathcal X$ 2) inverse transform $f^{-1}: \mathcal X \to \mathcal Z$ 3) likelihood의 3가지 interface로 구성한다. SurVAE Flows[8]에서는 stochastic transform에 대해서도 이에 맞게 구성할 수 있도록 framework를 확장한다.
- Forward Transform
conditional distribution $x\sim p(x|z)$를 상정한다. deterministic mapping에 대해서는 dirac delta를 통해 구성한다. $p(x|z) = \delta(x - f(z))$
- Inverse Transform
마찬가지로 deterministic mapping에 대해서는 $p(z|x) = \delta(z - f^{-1}(x))$를 상정한다. 반면에 stochastic mapping에 대해서는 $p(z|x)$의 연산이 intractable 하므로 variational $q(z|x)$를 상정하고 lower bound를 추정하는 식으로 접근한다.
- Likelihood
deterministic map과 stochastic map의 likelihood 구성은 다음과 같다.
$$\log p(x) = \log p(z) + \log|\det J|, \ \ z = f^{-1}(x)\\ \log p(x) = \log p(z) + \log \frac{p(x|z)}{q(z|x)} + \mathbb D_\mathrm{KL}[q(z|x)||p(z|x)], \ \ z \sim q(z|x)$$
이때 $|\det J|$는 $|\det \nabla_x f^{-1}(x)|$이다.
여기서 중요한 것은 framework를 확장하는 과정에서 deterministic transform의 분포를 Dirac delta $\delta(\cdot)$를 통해 구성하였고, 이를 기반으로 한 ELBO가 NF의 change of variables formulation과 같아진다는 것이다.
$$ p(x|z) = \delta(x - f(z)), \ \ p(z|x) = \delta(z - f^{-1}(x))$$ $$\begin{align*} \Rightarrow \log p(x) &= \log p(z) + \log|\det J| \\ &= \log p(z) + \log\frac{p(x|z)}{q(z|x)}\\ &\mathrm{where} \ \ q(z|x) = p(z|x) \end{align*}$$
정리하면 Change of variables의 전개는 ELBO에서 deriving 할 수 있고, VAE와 NF는 동일한 formulation을 통해 구성되는 하나의 확률 모형이었단 것이다. 이에 따라 둘은 forward와 inverse를 모두 stochastic transform으로 상정한 경우(VAE)와 모두 deterministic transform으로 상정한 경우(NF)의 mapping 방식에 따른 special case가 된다.
VAE와 NF가 precise 한 상관관계를 가진다는 것이 증명된 지점이다.
Theorem. Change of variables formula는 ELBO에서 deriving 가능하다.
pf. Dirac $\delta$-function을 통해 다음을 얻을 수 있다.
$$\int\delta(g(z))f(g(z))\left|\det\frac{\partial g(z)}{\partial z}\right|dz = \int\delta(u)f(u)du, \ \ u = g(z) \tag{1}$$ $$\exists! z_0: g(z_0) = 0 \Rightarrow \delta(g(z)) = \left|\det\frac{\partial g(z)}{\partial z}\right|_{z=z_0}^{-1}\delta(z-z_0) \tag{2}$$
(필자는 Eqn.1 좌항의 determinant term을 우항으로 옮기고, delta 함수가 trigging 되는 시점인 $z_0$의 determinant 값이 실체화되는 방식으로 이해함, dirac delta의 적분은 정의상 1이므로)
위 유도는 g가 미분가능하고, f는 compact support를 가지며, root는 unique하고, jacobian은 가역 행렬임을 가정한다.
$f: \mathcal Z \to \mathcal X$가 $f$와 $f^{-1}$ 모두에서 미분가능일 때 (i.e. diffeomorphism), deterministic conditionals에 대해 다음의 유도가 가능하다.
$$p(x|z) = \delta(x - f(z)), \ \ p(z|x) = \delta(z - f^{-1}(x)) \tag{3}$$ $$p(x|z) = \delta(z - f^{-1}(x))|\det J| = p(z|x)|\det J| \tag{4}$$
이때 jacobian은 $J^{-1} = \left.\partial f(z)/\partial z\right|_{z=f^{-1}(x)}$를 상정한다.
또한 deterministic transform에 따른 true posterior $p(z|x)$를 알고 있으므로, $q(z|x) = p(z|x) = \delta(z - f^{-1}(x))$에서 ELBO를 deriving 하면 다음과 같다.
$$\begin{align*}\log p(x) &= \mathbb E_{z\sim q(z|x)}\left[\log p(z) + \log\frac{p(x|z)}{q(z|x)} + \log\frac{q(z|x)}{p(z|x)}\right] \\ &= \log p(z) + \log|\det J|\end{align*}$$
이 과정에서 두 likelihood의 tractable한 contribution은 $\log[p(x|z)/q(z|x)] = \log|\det J|$에 따라 같아지고, variational posterior와 true posterior가 동치이므로 KL-term $\log[q(z|x)/p(z|x)] = 0$으로 소거된다.
Likelihood Contribution and Bound Gap
SurVAE Flows[8]는 이렇게 unifying 된 framework의 likelihood 연산을 위해 전체 term을 likelihood contribution $\mathcal V(x, z)$과 boundary gap $\mathcal E(x, z)$으로 분리한다. expectation은 single monte carlo sample에 대한 evaluation으로 대체한다.
$$\log p(x) \simeq \log p(z) + \mathcal V(x, z) + \mathcal E(x, z), \ \ z \sim q(z|x)$$
likelihood contribution은 전체 likelihood term 중에서 연산할 수 있고, 실제 gradient 기반의 optimization에 활용되는 부분이다. change of variables term $\log|\det J|$나 variational lower bound $\log[p(x|z)/q(z|x)]$가 이에 해당한다.
boundary gap은 lower bound estimation 과정에서 발생하는 true posterior와의 gap을 상정한다. VAE의 경우에는 $\log[q(z|x)/p(z|x)]$의 variational gap이 존재하고, NF의 경우에는 true posterior를 그대로 사용 가능하므로 0으로 소거된다.
이후 multiple layers에 대해서는 NF에서 compositional structure에 따라 각각의 log-determinant를 더해갔던 것처럼, stochastic map에 대해서도 동일하게 likelihood contribution을 더해가는 방식으로 일반화 가능할 것이다.

Algorithm 1: log-likelihood(x) (Nielsen et al., 2020)
SurVAE Flows
지금까지 framework 확장 과정에서 stochastic transform과 deterministic transform의 likelihood 연산 과정을 통합하고, 그를 위한 알고리즘을 구성해 보았다. 이 과정에서 NF는 forward, inverse가 모두 deterministic, VAE는 모두 stochastic 한 special case라는 것 또한 확인했다.
그렇다면 forward는 deterministic, inverse는 stochastic 하거나, inverse는 deterministic, forward는 stochastic한 케이스도 존재 가능한 것인가에 대한 의문이 있을 수 있다.
그리고 만약 위와 같은 구성이 가능하다면 bijective의 exact likelihood evaluation과 stochastic map의 dimension alternation 같은 이점들을 수집할 수 있는가에 대한 기대도 있을 것이다.
SurVAE Flows[8]의 저자들은 surjective transform을 통해 bijective와 stochastic map 사이의 격차를 메꿔보고자 했다.
우선 surjective이고 non-injective인 deterministic transform을 정의한다. 이는 이하 surjections 혹은 surjective transform으로 일컬을 것이다. 이렇게 surjections를 정의하게 되면 다수의 입력이 하나의 출력으로 매핑될 수 있고, 이 과정에서 inversion이 보장되지 않는다. 이에 저자들은 다음과 같은 interface를 구성한다.
- Forward Transform
bijective와 같이 dirac-delta를 통한 deterministic forward $p(x|z) = \delta(x - f(z))$를 상정한다.
- Inverse Transform
bijective와 달리 surjective $f: \mathcal Z \to \mathcal X$는 invertible 하지 않다. 이는 right inverse만 존재하고, left inverse는 존재하지 않기 때문이다. (i.e. $\exists g: \mathcal X \to \mathcal Z: \ f\circ g(x) = x \ \ \forall x\in \mathcal X$)
SurVAE Flows는 이에 stochastic right inverse를 inverse 대신 차용한다. $q(z|x)$의 stochastic posterior를 상정하고, $x$의 preimage 위에 support를 가지게 한다.
이렇게 되면 위에서 언급한 forward는 deterministic, inverse는 stochastic 한 케이스가 된다. 이를 generative surjections라 하고, 반대로 $\mathcal X \to \mathcal Z$ 방향에 surjections를 가정하면 forward는 stochastic, inverse는 deterministic 한 inference surjections가 된다.
- Likelihood Contribution
continuous surjections에 대한 likelihood contribution term은 다음과 같다.
$$\mathbb E_{q(z|x)}\left[\log\frac{p(x|z)}{q(z|x)}\right], \
\mathrm{as} \left\{\begin{matrix}
& p(x|z) \to \delta(x - f(z)), & \mathrm{for\ gen.\ surj} \\
& q(z|x) \to \delta(z - f^{-1}(x)), & \mathrm{for\ inf.\ surj}
\end{matrix}\right.$$
generative sujrections의 경우에는 stochastic posterior로 인해 likelihood의 lower bound를 추정해야 하지만, inference surjections의 경우에는 deterministic true posterior를 활용할 수 있으므로 exact likelihood evaluation이 가능하다.
이에 SurVAE Flows에서는 forward/inverse의 두 가지 방향과 deterministic/stochastic의 두 가지 mapping 방식에 대해 총 4가지 composable building blocks를 구성할 수 있다.

Table 1: Composable building blocks of SurVAE Flows (Nielsen et al., 2020)
Examples
- Tensor slicing
$z = (z_1, z_2) \in \mathbb R^d$에 대해 slice $x = f(z) = z_1$을 상정하면, 이는 generative surjections이다. 우선 이에 따른 forward와 inverse의 stochastic transformation을 정의한다.
$$p(x|z) = \mathcal N(x|z_1, \sigma^2I), \ \ q(z|x) = \mathcal N(z_1|x, \sigma^2I)q(z_2|x)$$
이때 $\sigma^2\to 0$이면 $p(x|z) \to \delta(x - f(z))$의 deterministic transform으로 수렴하므로 likelihood contribution은 다음과 같아진다.
$$\mathcal V(x, z) = \lim_{\sigma^2\to 0}\mathbb E_{q(z|x)}\left[\log\frac{p(x|z)}{q(z|x)}\right] = \mathbb E_{q(z_2|x)}[-\log q(z_2|x)]$$
그리고 이는 $q$의 entropy를 maximize 하는 방향으로 학습이 진행될 것이다. ANF[5]나 VFlow[6]에서 제안했던 augmentation과 동치이다.
반대로 $x = (x_1, x_2) \in \mathbb R^d$에 대한 slice $z = f(x) = x_1$을 상정한다면, 다음과 같이 inference surjections가 정의될 것이고, likelihood contribution은 $p(x|z)$가 $z$로부터 나머지 $x_2$를 복원하기 위한 형태로 구성될 것이다.
$$\mathcal V(x, z) = \mathbb E_{q(z|x)}\left[\log\frac{p(x|z)}{q(z|x)}\right] = \mathbb E_{p(z|x)}[\log p(x_2|z)]$$
- Rounding
rounding $x = \lfloor z\rfloor$를 상정하면, forward transform은 deterministic surjection으로 구성된다.
$$p(x|z) = \mathbb I(z \in \mathcal B(x)), \ \ \mathcal B(x) = \{x + u|u\in [0, 1)^d\}$$
inverse를 variational posterior$q(z|x)$에 대한 stochastic transform으로 구성하면, Flow++[4]에서 언급되었던 variational dequantization과 동치가 된다.
$$\mathcal V(x, z) = \mathbb E_{q(z|x)}[-\log q(z|x)]$$
- Absolute
$z = |x|$의 절댓값 연산을 상정한다면 이는 inference surjections이고, sign s에 대한 bernoulli 분포를 다루는 방식으로 작동할 것이다.
$$\begin{align*}&p(x|z) = \sum_{s\in\{-1, 1\}}p(x|z, s)p(s|z) = \sum_{s\in\{-1, 1\}}\delta(x - sz)p(s|z) \\\ &q(z|x) = \sum_{s\in\{-1, 1\}}q(z|x, s)p(s|x) = \sum_{s\in\{-1, 1\}}\delta(z - sx)\delta_{x, \mathrm{sign}(x)}\end{align*}$$
SurVAE Flows[8]는 그 외에도 flow framework에서 사용해볼 법한 몇 가지 layer를 더 제안한다. 이를 토대로 nonlinearities의 부재와 architecture의 constraint를 겪던 flow framework에 reasonable한 디자인을 추가할 수 있게 되었단 점에서 또 하나의 의의가 있을 것이다.
Connection to previous works
SurVAE Flows는 4가지 mapping 방식에 대한 generalized framework를 제안하면서 기존까지의 다양한 확률 모델과의 접점을 만들어 냈다.
bijective를 통한 modeling 과정에서 dimensionality, discrete data, misspecified prior에 대한 여러 문제점이 제기되었었고, 이에 따른 individual solutions를 하나의 framework 내에서 구성할 수 있게 된 것이다.

Table 3: SurVAE Flows as a unifying framework. (Nielsen et al., 2020)
Diffusion[9]은 이전 post에서 다뤘던 주제로, inverse에 noise를 더해가는 diffusion steps를 두고, forward에서 denoising을 objective로 하는 모델을 구성하는 방식이다. forward와 inverse가 모두 stochastic 한 formulation으로 구성된다.
Dequantization의 경우에는 continuous flow를 discrete data에 모델링하는 과정에서 degenerate point에 density가 몰리는 현상을 방지하고자, rounding operation을 상정하고 variational posterior를 통한 dequantization을 구성하는 method이다. 이는 rounding에 대한 generative surjections으로 구성된다. (post: Glow, Flow++)
ANF[5]와 VFlow[6]는 dimensionality problem의 해결을 위해 channel axis에 부가적인 latent를 부여하는 augmentation을 제안한다. 이는 tensor slicing에 대한 generative surjections로 구성된다. 반대로 RealNVP[2]에서 제안한 multi-scale architecture는 연산의 효율성을 위해 각 resolution에 대한 latent를 slicing 함으로 inference surjection에 해당한다. (post: NF, RealNVP, ANF, VFlow)
CIF[7]의 경우에는 misspecified prior를 활용한 상황에서의 real data fitting과 bi-Lipschitz constant에 대한 tradeoff를 보이며, 이에 대한 해결책으로 augmentation과 latent의 surjectivity를 통한 re-routing을 제안한다. 하지만 ANF[5], VFlow[6]와는 달리 hierarchy를 구성하므로 최종에서는 모든 latent를 사용하지 않고, re-routing에 해당하는 latent를 slicing 한다. (post: i-ResNet, CIF)
Experiments

Figure 4: Comparison of flows with and without absolute value surjections (Nielsen et al., 2020)
가장 먼저 한 실험은 symmetric data에서 실제로 absolute value surjection이 유용한가에 대한 실험이다. 실제로 동일한 flow에 absolute surjections를 추가한 것만으로 bits/dim이 줄어든 것을 확인할 수 있다.

Figure 5: Point cloud samples from permutation-invariant SurVAE Flows (Nielsen et al., 2020)
두 번째 실험은 SpatialMNIST에 대한 실험이다. point cloud는 집합으로 permutation-invariant 한 특성을 가진다. SurVAE Flows에서는 sorting surjections나 stochastic permutation을 통해 입력에 순서 정보를 제거할 수 있다. 또한 stochastic permutation에 대해서는 coupling layer에 positional encoding을 사용하지 않는 transformer를 활용함으로서 permutation invariant 한 모델을 구성했다.
실제로 PermuteFlow는 SortFlow에 비해 좋은 성능을 보였고, i.e. -5.30 vs -5.53 PPLL (per-point log-likelihood), 다른 non-autoregressive 모델에 비해서도 SOTA performance를 보였다.
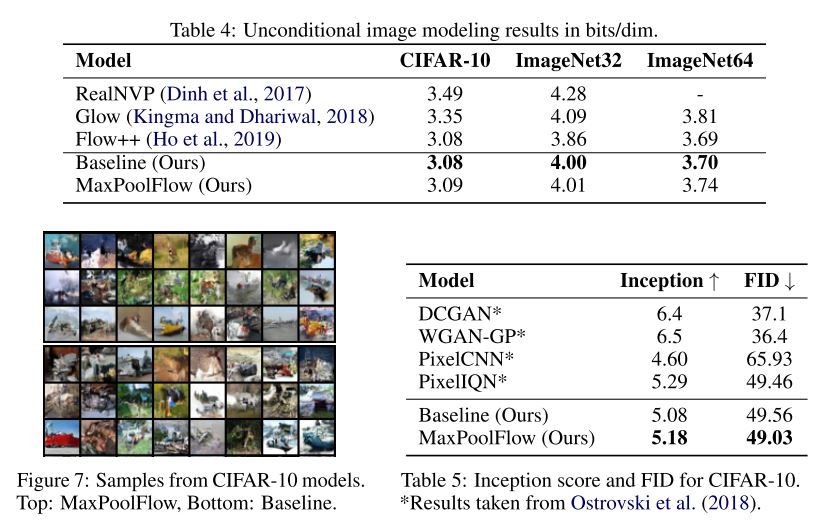
Modeling image data with MaxPoolFlow (Nielsen et al., 2020)
마지막은 이미지 데이터에 대해 max pooling을 활용하여 downsampling을 구성한 MaxPoolFlow이다. Baseline은 RealNVP[2]의 multi-scale architecture를 활용하였다.
실험 결과 slicing surjection에 비해 maxpool이 더 높은 bits/dim를 보이긴 했으나, IS/FID 에서는 더 좋은 visual quality를 갖는다 평가받았다.
Discussion
이로써 normalizing flow에 대해 기획했던 게시글을 모두 작성하였다.
NF에 대한 소개와 연구 초기에 소개되었던 RealNVP
어떤 layer와 architecture를 구성할지에 대해 소개했던 Glow, Flow++
dimensionality problem에 대한 해결책을 제시한 ANF, VFlow
residual network의 invertibility와 그 한계를 소개한 i-ResNet, CIF
마지막으로 모든 걸 unifying하고 NF의 새로운 지평을 연 SurVAE Flows
시작은 SurVAE Flows[8]를 접한 뒤였다. 당시 NF에 관심이 있었고, surjection을 통해 기존까지의 확률 모델 전반을 통합한 논문은 굉장한 호기심으로 다가왔다.
이를 위해 reference를 조사하고, 그렇게 하나둘 리뷰를 하던 중 연재물로써 NF의 글을 쓰고 다른 사람들과 공유할 수 있음 좋을 것 같다는 생각이 들었다.
하지만 글을 잘 쓰는 편도 아니고, 거의 논문을 번역해둔 듯한 글에 큰 의미가 있을까 고민도 했던 것 같다.
그래도 뭐라도 남겨두고, 한글로 되어 있음 참고할 사람은 참고할 수 있지 않을까 하는 생각이 들어 장장 5편의 NF 논문을 리뷰한 것 같다.
공부하면서 flow처럼 문제 제기와 해결, 추상화와 통합이 자연스레 순차적으로 이루어진 분야는 처음 보았다. 굉장히 많은 양의 머신러닝/딥러닝 관련 논문이 쏟아져 나오는 요즘, 이 정도의 스토리 라인을 구성할 수 있다는 점에서도 연구자분들에 대한 큰 감사함을 느낀다.
필자는 학부 휴학생 신분으로 음성 합성 연구를 시작하면서 연구는 어떻게 해야 하는지, 무엇을 만들어야 하는지에 대한 개념도 없이 일을 시작했던 것 같다. 그리고 1년 반, 2년 차가 되어가는 시점에서 flow를 공부한 것은 그 방향성을 잡는데에도 큰 도움을 준 것 같다.
그 외에도 NF라는 주제가 가지는 다양한 발전 가능성과 현실 세계에서의 적용 가능성에 대해 긍정적으로 바라보고 있고, 다양한 분들이 이 글을 통해 조금이나마 도움을 받았음 좋겠다.
Reference
[1] Rezende, D. J. and Mohamed, S. Variational inference with normalizing flows. In ICML 2015.
[2] Dinh, L., Sohl-Dickstein, J. and Bengio, S. Density estimation using Real NVP. In ICLR 2017.
[3] Kingma, D. P. and Dhariwal, P. Glow: Generative Flow with Invertible 1x1 Convolutions. In NIPS 2018.
[4] Ho, J. et al. Flow++: Improving flow-based generative models with variational dequantization and architecture design. In ICML 2019.
[5] Huang, C., Dinh, L. and Courville, A. Augmented Normalizing Flows: Bridging the Gap Between Generative Flows and Latent Variable models. 2020.
[6] Chen, J., et al. VFlow: More Expressive Generative Flows with Variational Data Augmentation. In ICML 2020.
[7] Cornish, R., Caterini, A., Deligiannidis, G., Doucet, A. Relaxing Bijectivity Constraints with Continuously Indexed Normalising Flows. In ICML 2020.
[8] Nielsen, D., Jaini, P., Hoogeboom, E., Winther, O., Welling, M. SurVAE Flows: Surjections to Bridge the Gap between VAEs and Flows. In NeurIPS 2020.
[9] Ho, J., Jain, A., Abbeel, P. Denoising Diffusion Probabilistic Models. In NeurIPS 2020.
[10] Kingma, P, D. and Welling, M. Auto-Encoding Variational Bayes. In ICLR 2014.