Rewriting a Deep Generative Model
- David Bau et al., 2020, arXiv
- Keyword: Generative, Adversarial learning
- Problem: How to manipulate specific rules encoded by a deep generative model.
- Solution: Projected gradient descent for adding rules to convolution of associative memory.
- Benefits: Enable users to synthesize edited new images by manipulating model only once.
- Contribution: Providing a new perspective of associative memory, rule manipulating method of projected gradient descent.
- Weakness or Future work: -
Generative model
생성 모델은 데이터의 분포를 학습하면서 여러 가지 규칙이나 관계를 만들어 나간다. 간단한 예로 ProgressiveGAN[1]이 만든 주방 이미지에서는 창문에서 오는 빛을 테이블에 반사시키는 경향이 있다.
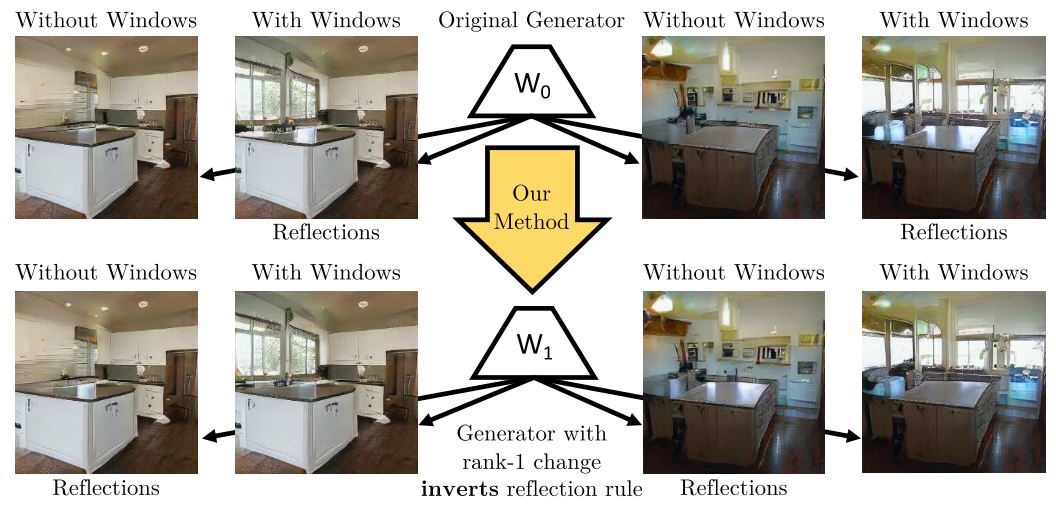
Fig. 6: Inverting a single semantic rule within a model
저자는 만약 이러한 규칙들을 직접 분석하여 수정할 수 있다면, 생성 모델 자체를 manipulating 하는 것이고, 이는 생성된 이미지를 각각 수정하는 것보다 효율적으로 수정된 이미지를 생성할 수 있다고 이야기 한다.
이를 위해서 우리는 생성 모델이 어떤 정보를 캡처하고 있고, 어떻게 unseen scenario에 대해 일반화 하고 있는지 알아야 한다.
현재 생성 모델들은 인간이 직접 라벨링 한 대규모의 데이터셋에 기반을 두고 있는데, 만약 manipulating 과정에서도 이러한 다량의 데이터와 학습이 추가로 필요하다면, 이는 손으로 생성된 이미지를 직접 수정하는 것과 큰 차이가 없을 것이다.
이에 우리는 단 몇 개의 샘플 데이터와 간단한 optimization을 통해 모델을 manipulation 할 수 있어야 하고, 이 모델은 우리가 원하는 rule을 캡처하여 unseen data에 대한 일반화를 할 수 있어야 한다.
저자는 이를 위해 sequential 하게 구성된 nonlinear convolutional generator를 associative memory라는 관점으로 해석하고, 전체 레이어가 아닌 단 하나의 레이어에 constrained optimization을 진행하여 기존의 semantic rule을 보존하면서, 우리가 원하는 rule을 추가할 수 있는 방법론을 제시한다.
Preview
pretrain된 generator $G(\cdot; \theta_0)$가 주어질 때, 모델은 각각의 latent $z_i$에 대해 $x_i = G(z_i; \theta_0)$의 output을 만들어 낸다. 만약 우리가 copy&paste 방식으로 변화를 준 output $x_{*i}$을 통해 새로운 rule을 표현한다면, rule의 표현 중 가장 직관적인 방법일 것이다.

Fig. 3: The Copy-Paste-Context interface for rewriting a model.
이때 하고자 하는 것은 새로운 rule을 따르는 $\theta_1$을 만드는 것이고, 이는 $x_{*i} \approx G(z_i; \theta_1)$을 만족할 것이다.
$\theta_1 = \arg\min_\theta \mathcal L_{\mathrm{smooth}}(\theta) + \lambda \mathcal L_\mathrm{constraint}(\theta)$
$\mathcal L_\mathrm{smooth}(\theta) \overset{\Delta}{=} \mathbb E_z[\mathcal l(G(z; \theta_0), G(z; \theta))]$
$\mathcal L_\mathrm{constraint}(\theta) \overset{\Delta}{=} \sum_i \mathcal l(x_{*i}, G(z_i; \theta))$
고전적인 해결책은 generator의 전체 parameter set $\theta_0$를 두 가지 constraint에 맞게 gradient 기반의 optimization을 진행하는 것이다. 이때 $\mathcal l(\cdot)$은 perceptual distance를 의미한다.
하지만 이 경우 몇 개 되지 않는 sample에 overfit될 가능성이 농후하며 다른 데이터에 대해 일반화되지 않을 수 있다.
이에 저자는 두 가지 방법론을 제안한다. 하나는 전체 parameter set이 아닌 특정 한 layer의 weight만을 update하는 것이고, 하나는 optimization을 특정 constraint 내에서 진행하는 것이다.
특정 layer L과 L-1 layer까지의 feature map k를 가정할 때 L의 output은 $v = f(k; W_0)$가 된다. 원본 이미지의 latent $z_{i}$가 feature $k_{*i}$를 만들 때 $v_i = f(k_{*i}; W_0)$를 가정하고, 직접 수정한 output에 대응하는 feature map $v_{*i}$를 구할 수 있으면 objective는 다음과 같다.
$W_1 = \arg\min_W \mathcal L_{\mathrm{smooth}}(W) + \lambda \mathcal L_\mathrm{constraint}(W)$
$\mathcal L_\mathrm{smooth}(W) \overset{\Delta}{=} \mathbb E_z[|| f(k; W_0) - f(k; W)||^2]$
$\mathcal L_\mathrm{constraint}(W) \overset{\Delta}{=} \sum_i ||v_{*i} - f(k_{*i}; W)||^2$
perceptual distance는 higher semantic을 표현하는 feature map 사이의 l2-distance를 상정한다. 이때 W만으로도 parameter의 양이 충분히 많을 수 있기에, overfit을 제한하면서 더 나은 일반화를 위해 학습 방향을 고정할 필요가 있었고, 특정 direction으로만 optimization 되도록 constraint를 추가한 gradient descent를 사용하였다.
Associative Memory
저자는 preview의 방법론을 associative memory로부터 유도해 낸다.
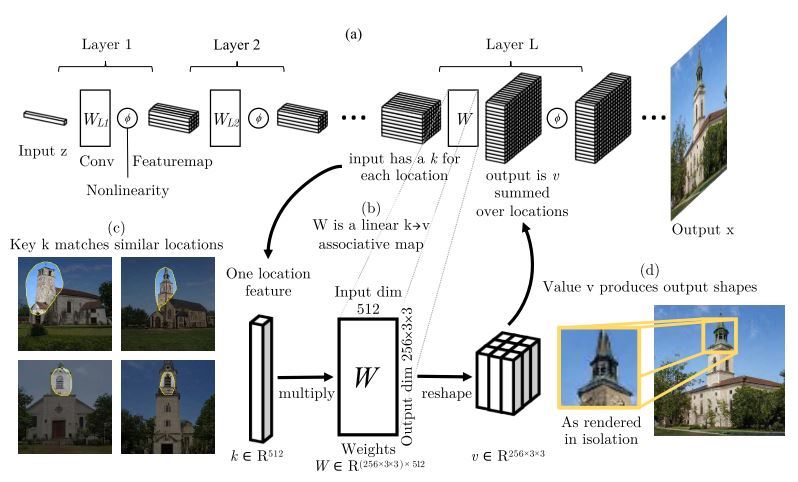
어떤 key $k_i \in \mathbb R^N$와 value $v_i \in \mathbb R^M$의 mapping $\{ k_i \to v_i \}_{i \in I}$을 가정하자. 이때 $k_i$가 mutually orthonormal 하면 i와 j가 다를 때 $k_i^T k_j = 0$를 만족한다. matrix W를 $W = \sum_i v_i k_i^T \in \mathbb R^{M \times N}$ 로 정의하면 orthogonality에 의해 $Wk_i = v_i$가 성립한다. 이를 key-value association을 기록한 memory라 하여 associative memory라고 부르며, linear operation으로 구성되므로 linear associative memory라 할 수 있다.
저자의 이야기는 Convolution 또한 associative memory의 일종으로 볼 수 있다는 것이다. 흔히 생각하는 convolution은 window에 대해 pixel-wise weighted sum을 한 결과를 나열하는 operation이다. 이는 output의 한 pixel을 관점으로 convolution을 해석한 것이다.
반대로 input feature에 대해 해석하면 single feature $k \in \mathbb R^{B\times N}$에 weight matrix $W \in \mathbb R^{N \times (MHW)}$를 곱하고, BxMxHxW의 2D tensor로 reshape 하여 location-aware summation 한 것으로도 볼 수 있다.
이렇게 되면 convolution은 kernel을 matrix로 보고 key가 orthogonal 할 때 linear associative memory로 해석될 수 있다.
Nonorthogonal Keys
key는 $\mathbb R^N$의 vector이므로 최대 N개까지 orthogonal 할 수 있고, 더 많은 key-value pair를 기록하기 위해서는 $v_i \approx Wk_i$를 approximately equal한 조건을 취하여 error를 minimizing 하는 방식으로 구성한다.
$W_0 \overset{\Delta}{=} \arg \min_W \sum_i ||v_i - Wk_i||^2$
이때 $K \overset\Delta= [k_1|…|k_S] \in \mathbb R^{N\times S}$ 와 $V \overset\Delta= [v_1|…|v_S] \in \mathbb R^{M\times S}$ 로 가정하면 multiple nonorthogonal key, value pair에 대한 associative memory를 구성할 수 있다.
$W_0 = \arg\min_W \sum_i||V - WK||^2$
그리고 이는 least square solution $W_0KK^T = VK^T$와 pseudo-inverse $K^+$에 대해 $W_0 = VK^+$로 표현된다.
What we want
즉 pretrain을 통해 구한 $W_0$는 trainset에서 연산한 L-1까지의 feature map과 그에 대한 response를 key-value로 가정한 associative memory가 된다.
여기서 우리가 하고 싶은 것은 다음과 같다.
user가 copy한 value와 paste한 지점의 key를 가져와 새로운 pair로 memory에 추가
이렇게 되면 L-1까지의 feature map에서 key가 관측되었을 때 memory에서 새로운 value가 mapping 되어 해당 부분에 copy한 context가 이미지에 발현된다. Model manipulation을 하는 주요한 근거가 되는 것이다.
이를 표현하면 $W_1 = \arg\min_W ||V - WK||^2$와 $v_* = W_1k_*$를 만족 시키는 constrained least-square (CLS) problem으로 구성되고, 이의 해는 다음과 같이 정리된다.
$W_1KK^T = VK^T + \Lambda k_*^T$
$W_1KK^T = W_0KK^T + \Lambda k_*^T$
$W_1 = W_0 + \Lambda(C^{-1}k_*)^T$
이 때 $C \overset\Delta= KK^T$로 구성하면 key가 zero-mean일 때 covariance로 해석될 수 있다. 결국 $\Lambda \in \mathbb R^M$를 구하는 문제로 귀결된다. 여기서 $d \overset\Delta= C^{-1}k_*$로 가정하면 $W_1 = W_0 + \Lambda d^T$로 볼 수 있고, 풀이는 다음과 같다.
$\left[ \begin{array}{c|c} W_1 & \Lambda \end{array} \right] \left[ \begin{array}{c|c} I & k_* \\ \hline -d^T & 0 \end{array} \right] = \left[ \begin{array}{c|c} W_0 & v_* \end{array}\right]$
$\left[ \begin{array}{c|c} W_1 & \Lambda \end{array} \right] = \left[ \begin{array}{c|c} W_0 & v_* \end{array} \right] \left[ \begin{array}{c|c} I & k_* \\ \hline -d^T & 0 \end{array} \right]^{-1}$
여기서 주목할 점은 2가지이다.
- user requested mapping $k_* \to v_*$의 soft error-minimization objective가 d라는 straight-line을 따라 update해야 하는 hard constraint로 바뀜
- direction d가 key에 의해서만 결정되고 value는 오직 user requested $v_*$가 $\Lambda$에 영향을 주는 방식 정도로만 작용함
결국 구현체에서는 covariance C 정도를 미리 연산하여 caching 해두고, request가 올 때 direction과 $\Lambda$를 계산하는 방식으로 작동할 것이다.
preview의 수식을 다시 들고오면, $W_1 = \arg\min_W ||V-WK||^2$는 smoothness를 위한 loss, $v_* = W_1k_*$는 constraint를 위한 loss로 볼 수 있다. 그리고 이 둘의 solution이 d라는 direction으로 update된 $W_1$로 나온 것이다.
Generalization
위까지의 정리는 copy&paste로 수정된 이미지에 대한 해당 layer와 그 전 layer의 response를 얻어와 key-value mapping을 구성할 수 있어야 한다. 하지만 SOTA를 이루고 있는 generative model들은 주로 gaussian noise에서 image로의 mapping을 확률적으로 학습하고 있기에, 수정된 이미지의 latent를 z-optimization을 통해 얻을 수 있어야 하고, 이 또한 rule이 크게 바뀐 경우에는 정확하지 않을 수 있다.
원문에서는 이 부분을 위해 feature independency를 보였는데, 일례로 stylegan과 progressive gan은 특정 레이어의 response를 patch로 나눠 주변 정보 없이 각각을 inference 했을 때도 원본과 유사한 object가 복원되었다는 것이다. 이는 feature map을 low resolution의 image로 보고 각 key가 해당 위치에 존재하는 object를 encoding 하고 있기에 가능하다는 가설을 세울 수 있다.

Fig. 17: Comparison of rendered cropped activations at various layers of Progres- sive GAN generated LSUN church images.
이렇게 되면 z-known image에서 복사하고자 하는 patch의 위치를 특정할 수 있을 때, low-resolution의 feature map에서 동일한 위치의 value를 가져와 대상에 위치만 맞춰 붙여넣으면 되고, feature map 수준에서 보다 perceptual 한 distance를 측정할 수 있게 된다.
만약 z와 convolutional response를 얻을 수 없어 image-level에서 distance를 측정해야 하거나, activation을 거친 response를 가정할 때에는 neural net의 nonlinearity에 의해 선형성 가정이 깨지게 된다. 이에 neural generator를 다루는 입장이라면 위 방법론이 nonlinear 환경에서 일반화될 수 있어야 한다.
원문에서는 nonlinear mapping $f(k; W)$가 있을 떄 update policy가 W의 row-space에 sensitive하고, column-space에 insensitive 하므로 동일한 rank-1 update를 $f(k_*; W) \approx v_*$의 optimization constraint로 쓸 수 있다고 한다.
linear phase에서는 $\Lambda$를 linear system을 통해 풀었다면, nonlinear phase에서는 gradient 기반의 optimization이 필요하다. 이때 $\Lambda$는 requested value와 direction에 의존하는 변수이기 때문에 이를 objective로 하는 optimization을 진행한다.
$\Lambda_1 = \arg\min_{\Lambda \in \mathbb R^M}||v_* - f(k_*; W_0 + \Lambda d^T)||$
만약 requested key-value pair가 하나가 아닌 여럿이라면, rank-1 대신 low-rank optimization이 될 것이고, S개 pair에 대해 다음과 같이 표현할 수 있다.
$d_i = C^{-1}K_{*i}$
$D_S \overset\Delta= [d_1|…|d_S]$
$\Lambda_S = \arg\min_{\Lambda \in \mathrm R^{M \times S}} || V_* - f(K_*; W_0 + \Lambda D_S^T)||$
그리고 update는 $W_S = W_0 + \Lambda_S D_S^T$로 이뤄질 것이다.
마지막으로 이 조건을 좀 더 relax하면 $\arg\min_W ||V_* - f(K_*; W)||$를 optimizing하고, 대신 매 step 마다 W를 $W_0 + \Lambda_S D_S^T$의 subspace로 projection 하는 projected gradient descent를 취한다.
Detail
original repository rewriting에서는 L-1까지의 feature map을 BHWxC로 reshape하여 collect_2nd_moment에서 z-dataset을 기반으로 CxC의 covariance를 미리 구해 놓는다.
이후 edit 요청이 들어오면 covariance_adjusted_query_key에서 direction을 구하는데, C의 pseudoinverse를 구하는 대신 $CD_S = K_S$의 least square solution (torch.lstsq)을 풀어 computational stability를 얻었다고 한다.
이때 전체 이미지에서 desired key만을 가져오기 위해 multi_key_from_selection에서는 target layer의 resolution에 맞게 image-level의 mask를 bilinear interpolation한 후, key matrix에 직접 곱하여 non-zero key만을 선별한다. feature independency에 따라 가능하다.
이후 $D_{S}$를 직접 이용하는 것이 아닌 low-rank subspace의 basis를 구해 활용하며, 원문에서는 SVD를 통해 eigen-value가 큰 eigen-vector를 선출하여 동일한 subspace를 구성하는 orthogonal basis로 활용했다.
이후 insert에서 parameter optimization을 진행한다.
weight은 subspace에 orthogonal 하게 변환하여 ortho_weight 변수에 저장해 둔다. 이는 projected_conv을 활용하는데, 흔히 gram-schmidt orthogonalization에서 하는 것과 같이 basis에 정사형한 벡터를 원본에서 빼는 방식으로 진행한다.
$W_\mathrm{ortho} = W - (WU_{1:R})U_{1:R}^T \ \mathrm{where} \ C^{-1}K_S = U\Sigma V^T, \ \mathrm{lowrank} \ R$
이후 feature-level distance를 L1으로 하는 optimization을 진행하고, 특정 스텝마다 weight을 subspace로 projection하여 ortho_weight에 더하는 방식으로 projected gradient descent를 구현한다.
이렇게 되면 optimization의 여파는 subspace 내에서만 구성되고, subspace에 orthogonal한 weight을 더함으로써 기존의 weight은 유지하고 subspace 내에서의 update만을 취할 수 있게 된다.
ZCA를 활용한 rank reduction은 원문의 Appendix. D.를 참고한다.
Layer selection
원문에서는 convolution layer를 neighbor와의 정보 취합으로 edge, texture, shape 등을 구별해 내는 관점보다는, 하나의 feature vector가 local patch가 되면서 주변과 disentangle 되는 관점을 취하였고, 이것이 memory model로 해석되었다.
원문에서는 실제로 ProgressiveGAN[1]과 StyleGANv2[2]의 일부 레이어에서 이런 feature 간 독립성을 띠고 있음을 보였다.
feature map을 MxN의 patch로 잘라 주변 정보 없이 적절한 크기의 output을 만들었을 때, 네트워크는 여전히 동일한 객체와 컨텍스트를 만들어 낼 수 있음을 보인다면, feature 간에 독립적인 정보를 담고 있음을 추론할 수 있다.
레이어마다 patch를 잘라 output을 만들었을 때 Frechet Inception Distance (FID)가 작다면 해당 patch는 주변 정보로부터 less dependence 한 것이고, FID가 높다면 dependent 한 것임을 나타낼 것이다.
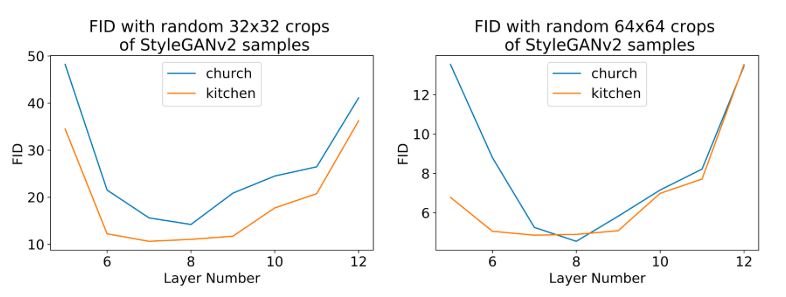
Fig. 13: FID of rendered cropped activations with respect to random crops of StyleGANv2 generated images
그래프에서 6~11번째 layer가 FID가 가장 낮았고, 이 layer에서 key 값은 주변과 independent 한 정보를 가지고 있을 확률이 높다. 즉, 어느 한 layer의 key를 수정해야 한다면, 해당 layer를 수정하는 것이 object를 render 하는데 좋은 quality의 이미지를 만들 수 있음을 나타낸다.

Fig. 14: Comparison of rendered cropped activations at various layers of Style- GANv2 generated LSUN church images.
Experiment
이제 User는 copy&paste를 통해 image에 원하는 부분을 수정하고 (key-value), 몇몇 context image에 수정되었으면 하는 부분(key-context)을 표기하여 rewriter에게 전달한다.
rewriter은 해당 key-context로부터 direction을 계산하고, pasted image와 original image 사이의 L1-loss를 기반으로 projected-optimization을 진행한다. 이에 따라 일반화된 model을 얻을 수 있고, editing을 마치게 된다.

Fig. 7: Giving horses a hat to wear.
Discussion
저자는 GPT-3, WaveNet과 같이 image 이외의 분야에서도 vastly trained model에 rule을 수정하고자 하는 일이 있을 것이고, model rewriting은 이 경우에 새로운 contents, behavior, interaction을 부여할 충분한 방법론일 것이라 이야기한다.
Implementation
- pytorch, official: David Bau, rewriting
- pytorch, unofficial: revsic, Rewriting-A-Deep-Generative-Models
References
- Progressive Growing of GANs for Improved Quality, Stability, and Variation, Tero Karras et al., 2017, arXiv:1710.10196.
- Analyzing and Improving the Image Quality of StyleGAN, Tero Karras et al., 2019. arXiv:1912.04958.