Invertible ResNet and CIF
- Invertible Residual Networks, Behrmann et al. In ICML 2019, arXiv.
- Relaxing Bijectivity Constraints with Continuously Indexed Normalising Flows, Cornish et al. In ICML 2020, arXiv.
- Keyword: Bayesian, Normalizing Flow, i-ResNet, ResFlow, Invertibel ResNet, CIF, Continuously Index Flows.
- Problem: Bijective and misspecified prior, topological mismatch.
- Solution: Surjective, augmentation, hierarchical structure.
- Benefits: Correcting misspecified posterior.
- Weakness or Future work: Is Augmented Flow can correct misspecified prior?
Series: Normalizing flow
- Normalizing flow, Real NVP [link]
- Glow, Flow++ [link]
- ANF, VFlow [link]
- i-ResNet, CIF [this]
- SurVAE Flows [link]
Residual Network
Neural network의 발전에 있어서 하나의 아키텍쳐로 여러 문제를 풀 수 있다는 것은 굉장한 이점으로 작용해 왔다. 하지만 근래에 들어서는 아키텍쳐의 발전이 domain-specific 하게 작용하고 있으며, 특히 VAE, Flow, GAN 등으로 나뉘어 발전한 generative task에서 이 점이 두드러진다.
그 중 discriminative task와 generative task의 여러 architecture design은 서로 다른 방향성을 띄어 갔고, 다양한 tuning 방법론들이 등장하며 점점 그 구성은 복잡해져만 갔다.
이에 저자들은 discriminative task와 generative task 모두에서 사용 가능한 어떤 universal architecture를 디자인하고자 했고, 그렇게 주목하게 된 구조가 invertible flow이다.
이번 글에서는 residual network의 invertibility와 free-form jacobian의 연산에 관해 이야기하고, Lipschitz-constraint와 invertible flow의 관계성, 한계의 해결방안에 대해 알아본다.
Enforcing Invertibility in ResNets
$$x_{t+1} \leftarrow x_t + g_{\theta_t}(x_t) \ \ \mathrm{where} \ x_t \in \mathbb R^d$$
residual block은 입력과 연산의 결과를 더하는 방식으로 구성된다. 이에 invertibility를 부여하기 위해서는 $x_{t+1}$이 주어졌을 때, $x_t$를 연산해 낼 수 있어야 한다.
$$x_t \leftarrow x_{t+1} - g_{\theta_t}(x_t)$$
Theorem 1. (Sufficient condition for invertible ResNets).
residual block은 Lipschitz-constant가 1보다 작을 때 invertible 하다.
$$\mathrm{Lip}(g_{\theta_t}) < 1$$
Remark. (Banach fixed point theorem)
complete metric space $(X, d)$에서 $T: X \to X$의 함수가 다음을 만족할 때 $T$를 contraction이라 한다.
$$\exists q \in [0, 1) : d(T(x), T(y)) \le qd(x, y) \ \forall x, y \in X$$
Banach fixed point theorem에 의해 contraction은 unique fixed point를 가지며, i.e. $\exists ! x^* \in X : T(x^*) = x^*$, 임의점 $x_0 \in X$으로부터 iteration을 통해 fixed point $x^*$를 찾을 수 있다.
$$\{x_n = T(x_{n-1})\}_{n\ge 1} \Rightarrow \lim _{n\to 1}{x_n} = x^*$$
pf.
Lipschitz-constant는 complete metric space $(X, d)$에서 어떤 함수 $T: X \to X$에 대해 다음과 같이 정의한다.
$$\mathrm{Lip}(T) = \inf \{q: d(T(x), T(y)) \le qd(x, y) \ \forall x, y \in X\}$$
이때 residual block의 inverse 연산을 contraction으로 본다면, $\mathrm{Lip}(x \mapsto x_{t+1} - g_{\theta_t}(x))$가 1보다 작아야 할 것이고, 이에 따라 unique fixed point $x^* = x_{t+1} - g_{\theta_t}(x^*)$가 존재할 것이다. 그리고 이 값은 유일하므로, inverse solution과 $x_t = x^ *$의 unique fixed point가 동치가 된다.
따라서 inverse 연산이 contraction이라면 fixed point iteration을 통해 이전 residual block의 출력값을 찾아낼 수 있고, l2-norm $||\cdot||_2$과 euclidean distance $d(x, y) = ||x - y||_2$에 대해 Lipschitz-constant의 제약을 풀어내면 다음과 같다.
$$\begin{align*} &\mathrm{Lip}(x \mapsto x_{t+1} - g_{\theta_t}(x)) \\ &= \inf \{q: d(x_{t+1} - g_{\theta_t}(x), x_{t+1} - g_{\theta_t}(y)) \le qd(x, y) \ \forall x, y \in X\} \\ &= \inf \{q: ||(x_{t+1} - g_{\theta_t}(x)) - (x_{t+1} - g_{\theta_t}(y))||_2 \le q||x - y||_2 \ \forall x, y \in X\} \\ &= \inf \{q: ||g _{\theta_t}(x) - g _{\theta_t}(y)||_2 \le q||x - y||_2 \ \forall x, y \in X\} \\ &= \inf \{q: d(g _{\theta_t}(x), g _{\theta_t}(y)) \le qd(x, y) \ \forall x, y \in X\} \\ &= \mathrm{Lip}(g _{\theta_t}) \lt 1 \end{align*}$$
즉 $g_{\theta_t}$의 Lipschitz-constant가 1보다 작을 때 residual block은 invertibility를 갖는다.
또한 fixed point iteration은 exponential scale에 따라 수렴하게 되므로, Lipschitz-constant가 작아질수록 더 적은 연산으로 unique point를 찾아낼 수 있다.
$$||x - x_n||_2 \le \frac{\mathrm{Lip}(g)^n}{1 - \mathrm{Lip}(g)}||x_1 - x_0||_2$$
Satisfying the Lipschitz Constraint
i-ResNet[1]에서는 residual block을 contractive nonlinearities (e.g. ReLU, ELU, tanh)와 convolution으로 구성한다.
SN-GAN[3]에서는 정의에 따라 matrix A에 대한 spectral norm $\sigma(\cdot)$을 largest singular value of A로 연산하고, linear transform $g$의 Lipschitz norm $\mathrm{Lip}(g) = ||g||_\mathrm{Lip}$을 다음과 같이 보인다.
$$||g||_\mathrm{Lip} = \sup_h \sigma(\nabla g(h)) = \sup_h \sigma(W) = \sigma(W)$$
이에 따라 convolution으로 구성된 residual block이 Lipschitz-constant를 만족하기 위해서는 각각의 convolutional weights에 spectral norm을 취해 1 이하로 둘 수 있어야 한다. contractive nonlinearities $\phi$를 상정한다면 전개는 다음과 같다.
$$\mathrm{since} \ ||g_1 \circ g_2||_\mathrm{Lip} \le ||g_1|| _\mathrm{Lip}||g_2|| _\mathrm{Lip}, \\ ||W_2\phi(W_1)|| _\mathrm{Lip} \le ||W_2|| _\mathrm{Lip}||\phi|| _\mathrm{Lip}||W_1|| _\mathrm{Lip} \le ||W_2|| _\mathrm{Lip}||W_1|| _\mathrm{Lip} \\ \Rightarrow \mathrm{Lip}(g) \le 1, \ \ \mathrm{if} \ ||W_i|| _\mathrm{Lip} \le 1$$
Spectral norm은 power-iteration 방식으로 근사하여 취급한다.
Determinant of Free-form Jacobian
invertible resnet, 이하 i-ResNet[1]은 jacboian의 norm에 일정 constraint를 요구하지만, coupling layer와 같이 matrix의 form 자체에 제약을 걸지는 않는다. 따라서 기본적으로 determinant 연산까지 $\mathcal O(d^3)$의 cubic complexity를 가정해야 하고, 이에 high-dimensional data에서는 intractable 하다는 문제를 가진다.
이에 log-determinant term 자체를 효율적으로 근사하기 위한 방법론이 필요하다.
우선 data $x$와 prior $z \sim p_z(z)$에 대해 Lipschitz-constrained $F(x) = x + g(x)$를 상정한다. $F$는 invertible하고, $z = F(x)$로 둘 때 change of variables에 의한 likelihood 전개가 가능하다.
$$\ln p_x(x) = \ln p_z(z) + \ln|\det J_F(x)|$$
이때 eigen values $\lambda_i$와 다음의 전개에 따라 determinants를 양수로 상정할 수 있다.
$$\begin{align*} & \lambda_i(J_F) = \lambda_i(J_g) + 1 \land \mathrm{Lip}(g) < 1 \\ & \Rightarrow |\lambda_i(J_g)| < 1 \\ & \Rightarrow \det J_F = \Pi_i(\lambda_i(J_g) + 1) > 0 \end{align*}$$
또한 non-singual matrix A에 대해 $\ln\det(A) = \mathrm{tr}(\ln(A))$ 이므로, trace of matrix logarithm의 power series에 의해 다음과 같은 전개가 가능하다.
$$\begin{align*} \ln p_x(x) &= \ln p_z(z) + \mathrm{tr}(\ln(I + J_g(x))) \\ &= \ln p_z(z) + \sum^\infty_{k=1}(-1)^{k+1}\frac{\mathrm{tr}(J_g^k)}{k} \end{align*}$$
이에는 여전히 computational drawbacks가 존재하는데, 1) trace of jacobian을 square complexity로 상정하거나, d개 diagonal entry에 대해 g를 매번 연산하여 더해야 하고 2) matrix power가 필요하며 3) series가 무한하다는 것이다.
이 중 1)은 automatic differentiation 과정에서 연산량을 줄일 수 있고, 2) matrix trace는 $v \sim N(0, I)$를 통해 stochastic approximation이 가능하다고 한다.
$$\mathrm{tr}(A) = \mathbb E_{p(v)}[v^TAv]$$
지금까지는 unbiased estimation을 상정했지만, 3)의 해결을 위해 infinite series의 truncation이 불가피하고, approximation 과정에서 biased estimator로 변모한다.
n-th truncation error는 다음에 의해 상한을 가진다.
$$\left|\sum^\infty_{k=n+1}(-1)^{k+1}\frac{\mathrm{tr}(J_g^k)}{k}\right| \le \sum^\infty_{k=n+1}\left|\frac{\mathrm{tr}(J_g^k)}{k}\right| \le d\sum^\infty_{k=n+1}\frac{\mathrm{Lip}(g)^k}{k} \\ \mathrm{since} \ \sum^\infty_{k=1}\frac{\mathrm{Lip}(g)^k}{k} = -\ln (1 - \mathrm{Lip}(g)) \\ d\sum^\infty_{k=n+1}\frac{\mathrm{Lip}(g)^k}{k} = -d\left(\ln(1 - \mathrm{Lip}(g)) + \sum^n_{k=1}\frac{\mathrm{Lip}(g)^k}{k}\right)$$
이는 추후 ResFlow[2]라는 후속 논문에서 russian roullete estimation을 통해 unbiased estimation을 구현해 내고, softplus나 elu의 vanishing second order derivatives 현상과 training instability를 보완하기 위해 LipSwish를 제안하기도 한다.
Lipschitz Constraints and Pushforwards
(이하는 개인의 이해보다는 논문의 표기를 그대로 따르며, 내용의 소개 정도를 목표로 한다.)
Normalizing flow는 density estimation의 pushforward에 해당한다. 이는 prior measure $P_Z$와 bijective $f: \mathcal Z \to \mathcal X$에 대해 measure $P_X := f \# P_Z := P_Z\circ f^{-1}$를 정의한다.
topological view에서 support of $P_Z$는 직관적으로 $P_Z$가 밀도를 할당하고 있는 region of $\mathcal Z$를 의미한다. 따라서 target $P_X^*$와 pushforward $P_X$가 완벽히 일치하기 위해서는 두 support가 동치여야 한다. ($\overline A$는 closure of A이다.)
$$\mathrm{supp} P_X^* = \overline{f(\mathrm{supp}P_Z)}$$
이때 normalizing flow는 bijective f를 가정하므로, 두 support가 일치하기 위해서는 $P_X^*$와 $P_Z$의 support가 homeomorphic 해야 한다 (i.e. topological space에서의 isomorphic을 의미한다.).
$$\mathrm{supp}P_X = \mathrm{supp}P_X^* \ \ \mathrm{only \ if} \ \mathrm{supp} P_Z \simeq \mathrm{supp} P_X^*$$
이 의미는 $P_Z$와 $P_X^*$의 support가 같은 topological properties를 공유한다는 것인데, 예를 들면 holes, knots, connected components의 수가 같아야 한다.
따라서 현재 단순 gaussian prior를 상정한 normalizing flow는 complex real-world densities를 학습하기에 topological mismatch의 불가항력이 존재한다.
이 condition을 완화하기 위해서는 $P_X \approx P_X^*$로 두어 topological misspecified prior를 사용할 수 있게 하거나, pushforward f의 bijectivity를 완화해야 할 수 있어야 한다.
Behrmann et al. (2020)[4]에서는 numerical invertibility의 척도로 bi-Lipschitz constant를 상정한다. ([4]에서는 수학적으로 잘 정의된 inverse도 precision의 한계를 가지는 머신 위에서 numerical inverse가 명확하지 않을 수 있음을 보인다.)
$$\mathrm{BiLip} f = \max \left( \mathrm{Lip}(f), \mathrm{Lip}(f^{-1}) \right)$$
bi-Lipschitz constant는 $f$나 $f^{-1}$가 한 번에 jump 할 수 있는 정도를 의미한다. 이때 $f$가 injective하지 않으면 $\mathrm{BiLip} f = \infty$이고, $\mathrm{BiLip} f < \infty$이면 $f$는 homeomorphism이다.
다음은 $P_Z$와 $P_X^*$가 homeomorphic하지 않을 때 $f$의 bi-Lipschitz constant가 근사를 위해 임의로 커질 수 있음을 의미한다.
Theorem 2.1. $P_Z$와 $P_X^*$가 $\mathbb R^{d_\mathcal{Z}}$와 $\mathbb R^{d_\mathcal X}$의 measure이고, $\mathrm{supp}P_Z \not\simeq \mathrm{supp}P_X^ *$일 때, sequence of measurable $f_n: \mathbb R^{d_\mathcal{Z}} \to \mathbb R^{d_\mathcal X}$에 대해 $\lim_{n\to\infty}\mathrm{BiLip}f_n = \infty$이어야만 $f_n\#P_Z \overset{D}{\to} P_X^ *$이 만족한다.
이 때 $\overset{D}{\to}$는 weak convergence이며, 이는 KL, JS, Wasserstein metric과 같은 statistical divergence의 minimisation을 의미한다. Theorem2.1.은 다른 말로 bi-Lipschitz constant가 임의로 커질 수 있어야 pushforward가 원하는 measure에 수렴할 수 있음을 이야기한다. 또한 이 과정에서 $d_\mathcal Z = d_\mathcal X$를 가정하지 않으므로 GAN과 같은 injective pushforward를 포함한다.
Practical Implication
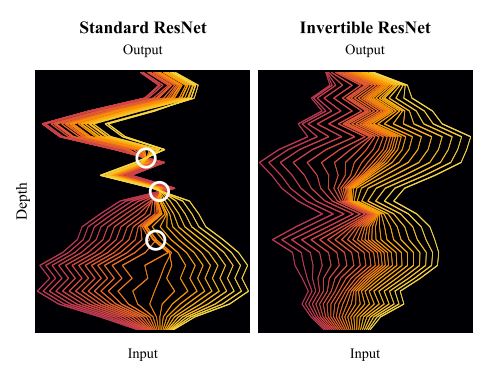
이 정리의 가장 직접적인 영향을 받는 것이 i-ResNet[1]과 ResFlow[2]이다. 이들은 invertibility를 위해 spectral normalization으로 residual layer의 Lipschitz-constant가 1 이하가 되도록 구성하였다.
$$f^{-1}_l(x) = x + g_l(x), \ \ \mathrm{Lip}(g_l) \le \kappa < 1$$
i-ResNet[1]의 Lemma2에서는 이를 토대로 bi-Lipschitz constant의 upperbound를 구하게 되며, 이것이 Theorem 2.1.에 의해 non-homeomorphic prior $P_Z$의 근사에 제약이 발생함을 의미한다.
$$\mathrm{BiLip}f\le\max(1+\kappa, (1 - \kappa)^{-1})^L < \infty$$
이는 $\kappa\to1$을 통해 relax 할 수 있을 것으로 보이나, 반대로 russian roullete estimator의 variance를 높여 determinant의 수렴을 어렵게 한다. $L\to\infty$를 상정한다면, layer 수의 증가를 의미하므로 computational cost의 증대로 이어진다.
그 외의 대부분 normalizing flow는 architecture에 bi-Lipschitz constraint를 걸지 않으므로, Theorem2.1.의 영향을 받지 않는다.
반면 Behrmann et al. (2020)[4]에서는 well-defined inverse에서도 numerically noninvertible 할 수 있기에, 명시적으로 $\mathrm{BiLip}f$를 제약하라고 제안하기도 한다. 즉 Theorem2.1.은 expressivity에 대한 numerical stability와 layer 수의 fundamental tradeoff를 시사한다.
CIF: Continuously Indexed Flow
이에 대해 CIF, Continuously Indexed Flow[7]는 ANF[5]와 VFlow[6] 때와 같이 augmentation을 그 해결책으로 제안한다.
CIF[7]는 coninuous index $\mathcal U \subseteq \mathbb R^{d_\mathcal U}$와 bijective indexed family $\{F(\cdot;u): \mathcal Z \to \mathcal X\}_{u\in \mathcal U}$를 상정한다. 이에 대한 generative process는 다음과 같다.
$$Z\sim P_Z, \ \ U \sim P_{U|Z}(\cdot|Z), \ \ X := F(Z; U)$$
저자들은 bijective f를 통해 $p_{U|Z}$와 $F$를 다음과 같이 모델링한다.
$$p_{U|Z}(\cdot|z) = \mathrm{Normal}(\mu^p(z), \Sigma^p(z)) \\ F(z; u) = f(\exp(-s(u)) \odot z - t(u))$$
여기서 $F^{-1}$를 활용해 likelihood를 구성하면 다음과 같다.
$$z = F^{-1}(x; u) \\ p_{X, U}(x, u) = p_Z(z)p_{U|Z}(u|z)|\det DF^{-1}(x; u)|$$
이에 대한 marginal은 intractable 하므로 variational posterior $q_{U|X}$를 두어 lower bound를 추정한다.
$$\mathcal L(x):= \mathbb E_{u\sim q_{U|X}(\cdot|x)}\left[\log\frac{p_{X, U}(x, u)}{q_{U|X}(u|x)}\right] \\ q_{U|X}(\cdot|x) = \mathrm{Normal}(\mu^q(x), \Sigma^q(x))$$
이는 augmented flow로 추상화할 수 있는데, VFlow[6]에서는 latent u를 conditional flow로 모델링했다면, CIF[7]에서는 단순 gaussian으로 모델링 한 것이고, VFlow[6]에서 multiple coupling block을 두어 latent u와 data x사이의 정보 공유를 상정했다면, CIF[7]에서는 latent u만이 x의 모델링에 관여하는 single coupling block을 상정했다고 볼 수 있다.
단 이렇게 되면 이전 augmented flow의 post에서도 이야기하였듯 u와 x 사이에 hierarchy가 발생하여 bottleneck problem의 해결로 이어지긴 어려울 듯하다.
그럼에도 CIF[7]에서 hierarchy와 augmentation을 상정한 이유는 다음의 두 가지 정리 떄문이다.
Proposition 4.1. $\phi \in \Theta$에 대해 $f: \mathcal Z \to \mathcal X, F_\phi(\cdot; u) = f(\cdot) \ \ \forall u \in \mathcal U$를 가정한다. 그럼 density $r$ on $\mathcal U$에 대해 trivial posterior $p^\phi_{U|Z}(\cdot|z) = q^\phi_{U|X}(\cdot|x) = r(\cdot) \ \ \forall z \in \mathcal Z, x \in \mathcal X$에도 다음이 만족한다.
$$D_\mathrm{KL}(P^*_X||P^\theta_X) \le D _\mathrm{KL}(P^ *_X||f\#P_Z) \ \ \mathrm{if} \ \ \mathbb E _{x\sim P_X^ *}[\mathcal L^\theta(x)] \ge \mathbb E _{x\sim P^ *_X}[\mathcal L^\phi(x)]$$
이는 trivial posterior를 통해 likelihood의 lower-bound를 가정할 때, 학습된 모델이 KL divergence라는 measure에 대해 더 잘 작동한다는 것을 의미한다.
CIF[7]에서는 이 현상을 $P_{U|Z}$를 통해 $P_X^*$의 support 외부에 존재할 수 있는 z를 rerounting 할 수 있었기 때문이라고 이야기한다. 예로 $z\in \mathcal Z$와 $f$에 대해 $f(x) \in \mathrm{supp} P_X^ *$라면 $F(z;u) = f(z) \ \ \forall u \in \mathcal U$로, $f(z) \not\in \mathrm{supp} P_X^ *$더라도 $F(z; U) \in \mathrm{supp}P_X^ *$를 구성할 수 있도록 $P_{U|Z}(\cdot|z)$의 support가 $\{u\in \mathcal U: F(z; u) \in \mathrm{supp}P_X^ *\}$에 존재하게 하는 것이다.
물론 이 과정에서 f가 충분히 단순하다면, $P_{U|Z}$는 굉장히 complex 해질 것이고, ELBO가 loose 해져 performance 역시 떨어질 것이다. 저자들은 이를 방지하기 위해 f를 10-layer ResFlow 같이 충분히 complex 한 모델을 상정하고, 일부 누수가 생기는 것을 $P_{U|Z}$가 보정하는 정도의 역할을 부여받을 수 있게 구성했다.
Proposition 4.3. $F(z;\cdot): \mathcal U \to \mathcal X$가 모든 $z\in\mathcal Z$에 대해 surjective이면 $P_{U|Z}$가 존재하여 $P_X=P_X^*$이다.
물론 CIF[7]에서 제안한 component들이 위 조건을 필수적으로 만족하거나, variational posterior가 충분히 expressive 하지 않았을 수 있다. 하지만 최소한 misspecified prior를 수정하기 위한 mechanism을 제안한 점에서 의의가 있다.
ANF[5], VFlow[6]와의 차이가 있다면, 기존의 augmented flow는 마지막에 [z, u] 모두를 latent로 차용하지만, CIF[7]는 z만을 latent로 활용하여 u에 대한 slicing을 구성한다. hierarchy에 따라 bottleneck을 해결하지 못하더라도 surjectivity에 따른 misspecified prior의 수정을 수식적으로 증명했음에 또 다른 의의가 있다.
Experiments

Table 2. Comparison of i-ResNet to a ResNet-164 baseline architecture. (Behrmann et al., 2019)

Table 4. MNIST and CIFAR10 bits/dim results. (Behrmann et al., 2019)
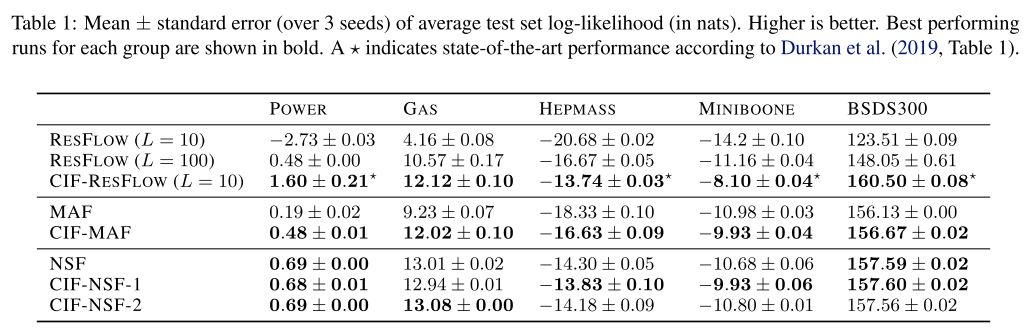
Table 1: Mean ± standard error (over 3 seeds) of average test set log-likelihood (in nats). Higher is better. (Cornish et al., 2020)
Discussion
(사견)
꽤 긴 시간 공부해서 글을 쓰게 되었다. 정확한 이야기를 전달하고 싶었지만, 유난히 확신이 서지 않는다.
Normalizing flow는 bijectivity를 근간으로 하기에, prior와 real data 사이의 topological mismatch를 bi-Lipschitz constant를 발산시킴으로써 해결해야 했다.
이 과정에서 precision 상 한계를 가진 머신은 inversion에 numerical stability를 보장하지 못한다는 문제가 제기되었고, 이 해결책으로 bi-Lipschitz constant를 제한하자면서 trade-off의 관계가 발생했다.
CIF[7]는 이를 위해 normalizing flow에 hierarchy를 구성하고, additional latent를 통해 misspecified prior의 보정이 가능함을 이야기하였다.
개인적으로는 이러한 surjective의 전제와 증명이 ANF[5]나 VFlow[6]의 성능을 증명하는 것에도 활용될 수 있을 것으로 보인다.
이렇게 Normalizing flow의 여러 문제와 해결안이 제기되고 있고, 그에 augmentation과 surjectivity가 종종 등장하고 있다. 추후 연구에서도 이를 통해 다른 확률 모델과의 연관성이나 universality 같은 이야기가 충분히 이뤄져 이제는 “왜 되는지 아는 모델"의 한 축이 되었음 좋겠다.
Reference
[1] Behrmann, J., Grathwohl, W., Chen, T. Q., Duvenaud, D. and Jacobsen, J.-H. Invertible Residual Networks. In ICML 2019.
[2] Chen, T. Q., Behrmann, J., Duvenaud, D. and Jacobsen, J.-H. Residual Flows for Invertible Generative Modeling. In NeurIPS 2019.
[3] Miyato, T., Katoka, T., Koyama, M. and Yoshida, Y. Spectral Normalization for Generative Adversarial Networks. In ICLR 2018.
[4] Behrmann, J., Vicol, P., Wang, K.-C., Grosse, R. B., Jacobsen, J.-H. On the Invertibility of Invertible Neural networks. 2019.
[5] Huang, C., Dinh, L. and Courville, A. Augmented Normalizing Flows: Bridging the Gap Between Generative Flows and Latent Variable models. 2020.
[6] Chen, J., et al. VFlow: More Expressive Generative Flows with Variational Data Augmentation. In ICML 2020.
[7] Cornish, R., Caterini, A., Deligiannidis, G., Doucet, A. Relaxing Bijectivity Constraints with Continuously Indexed Normalising Flows. In ICML 2020.