Normalizing Flow, Real NVP
- Variational Inference with Normalizing Flows, Rezende and Mohamed, 2015, arXiv
- Density Estimation using Real NVP, Dinh et al., 2017, arXiv
- Keyword: Bayesian, Normalizing Flow, Real NVP
- Problem: inflexibility of variational posterior
- Solution: probabilistic modeling with bijective and change of variables
- Benefits: simple sampling, exact log-likelihood estimation
- Weakness or Future work: determinant, inverse and architecutral constraint
Series: Normalizing flow
- Normalizing flow, Real NVP [this]
- Glow, Flow++ [link]
- ANF, VFlow [link]
- i-ResNet, CIF [link]
- SurVAE Flows [link]
Variational Inference
우리는 데이터에 대한 insight를 얻고자 할 때 probabilistic modeling을 통해 데이터가 어떤 분포를 가지는지 추정한다. 그 과정에서 latent variable을 도입하기도 하고, marginalize 과정에서 발생하는 적분의 intractability로 인해 variational inference를 활용해 posterior를 known distribution으로 근사하기도 한다.
$$\log p_\theta(x^{(i)}) = D_{KL}(q_\phi(z|x^{(i)})||p_\theta(z|x^{(i)})) + \mathbb E_{q_\phi}\left[ \log \frac{p_\theta(x, z)}{q_\phi(z|x)} \right]$$
이 중 연산이 가능한 두번째 RHS term만을 발췌해 variational lower bound라 부른다.
$$\log p_\theta(x^{(i)}) \ge \mathbb E_{q_\phi}\left[\log\frac{p_\theta(x, z)}{q_\phi(z|x)}\right] = \mathbb E_{q_\phi(z|x^{(i)})}\left[ \log p_\theta(x^{(i)}|z) \right] - D_{KL}(q_\phi(z|x^{(i)})||p_\theta(z))$$
Rezende & Mohamed(2015)[1]에서는 성공적인 variational inference를 위해 1) derivatives of log-likelihood $\nabla_\phi\mathbb E_{q_\phi(z)}\left[\log p_\theta(x|z)\right]$ 연산의 효율성과 2) approximate posterior $q(\cdot)$의 유연함이 필요하다 이야기한다.
전자의 경우에는 VAE[2]에서와 같이 Monte carlo approximation과 reparametrization을 통해 gradient를 연산하는 방식을 취할 수 있다.
$$z \sim \mathcal N(z|\mu, \sigma^2) \Leftrightarrow z = \mu + \sigma \epsilon, \ \ \epsilon \sim \mathcal N(0, 1) $$
하지만 이렇게 되면 variational posterior가 gaussian과 같은 분포로 한정되고, 이 경우 true posterior로의 근사가 어려울 수 있다.
따라서 이상적인 variational distribution $q_\phi(z|x)$는 true posterior의 근사를 위해 highly flexible해야 하고, 저자는 그 solution으로 normalizing flow를 제안한다.
Normalizing Flow
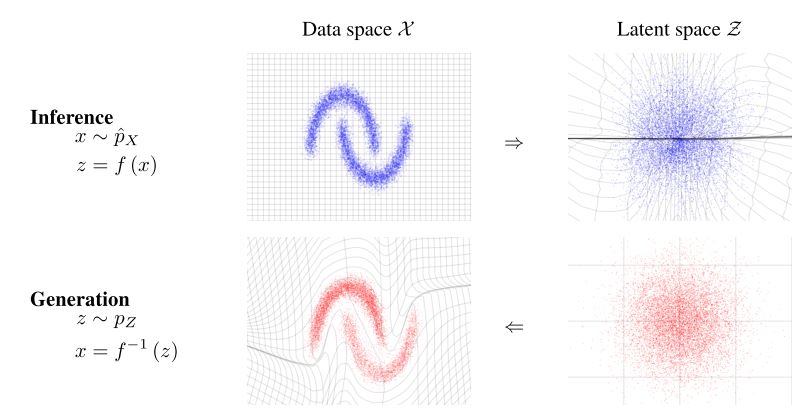
Normalizing flow는 invertible map을 통해 probability density를 순차적으로 변형시켜 나가는 모델이다. 각각의 invertible map은 change of variables를 통해 initial density를 변형시켜 나가고, density의 변환 흐름, ‘flow’를 표현하게 된다.
Change of variables
확률변수 $X \in \mathbb R^d$의 CDF $F_X$와 어떤 단조함수 $g: \mathbb R^d \to \mathbb R^d$에 대해 $Y=g(X)$이면, 다음이 성립한다.
$$F_Y(y) = P(Y \le y) = P(g(X) \le y) = P(X \le g^{-1}(y)) = F_X(g^{-1}(y))$$
이때 양변을 미분하면 $Y$에 대한 density를 구할 수 있게 되고, sample에 대한 exact log-likliehood의 연산이 가능해진다.
$$f_Y(y) = f_X(g^{-1}(y))\left|\det\frac{\partial g^{-1}}{\partial y}\right| \\ \log f_Y(y) = \log f_X(g^{-1}(y)) + \log\left|\det\frac{\partial g^{-1}}{\partial y}\right|$$
Finite Flows
Normalizing flow는 simple invertible map을 순차적으로 합성해 나가며 initial density를 임의의 complex distribution으로 만들어나간다.
initial random variable $z_0$와 distribution $q_0$에 대해 sequence of invertible map $f_1, …, f_K$을 chain으로 구성하면 $x=z_k$의 sampling과 exact log-likelihood의 연산이 가능하다.
$$z_K = f_K \circ \ … \ \circ f_2 \circ f_1(z_0) \\ \ln q_K(z_K) = \ln q_0(z_0) - \sum^K_{k=1}\ln\left|\det\frac{\partial f_k}{\partial z_{k-1}}\right|$$
이때 initial distribution $q_0(z_0)$부터 $z_k = f_k(z_{k-1})$로 구성된 path를 flow라 한다.
이는 LOTUS(law of unconscious statistician)으로도 불리며, 이 경우 $q_K$로 구성된 expectation을 분포에 대한 정보가 없이 연산 할 수 있게 된다. 이를 활용해 posterior를 모델링 하면 최종 분포상 제약이 없어 보다 유연한 근사가 가능하다.
또한 기존의 확률 모델이 complexity를 높이기 위해 nonlinear transform을 활용하면서 invertibility를 포기하고, ELBO를 통해 log-likelihood의 lower bound를 추정했다면,
nomarlizing flow는 NN을 활용한 engineered linear transform을 순차적으로 적용해 나가며 exact log-likelihood의 연산과 single forward-pass의 sampling이 가능하다는 것에 의의가 있다.
Real NVP: Modeling bijectivity
Normalizing flow는 여러가지 이점을 가지는 대신에 determinant와 inverse map이 tractable 해야 한다는 architecture의 constraint를 가진다.
RealNVP[3]는 이러한 constraint에 대해 well-engineered transform을 제안한다.
- Coupling layers
determinant와 jacobian을 고차원 데이터와 함수에 대해 연산한다는 것은 일반적으로 굉장히 computationally expensive하다. 이를 위해서 RealNVP[3]가 한 선택은 bijective에 제약을 가하여 jacobian을 triangular matrix로 구성하는 것이다.
Affine coupling layer은 D-dimensional input $x \in \mathbb R^D$에서 $d \lt D$의 일부 $x_{1:d}$를 활용하여 나머지 $x_{d+1:D}$를 affine transform한다.
$$y_{1:d} = x_{1:d} \\ y_{d+1:D} = x_{d+1:D} \cdot \exp(s(x_{1:d})) + t(x_{1:d})$$
이때 $s$와 $t$는 NN으로 구성한 scale과 translation function $\mathbb R^d \mapsto \mathbb R^{D-d}$이다.
이 경우 jacobian matrix는 lower-triangular matrix로 구성되고, log-determinant는 scale의 합으로 연산된다.
$$\frac{\partial y}{\partial x} = \left[ \begin{matrix} \mathbb I_d & 0 \\ \frac{\partial y_{d+1:D}}{\partial x_{1:d}} & \mathrm{diag}(\exp(s(x_{1:d}))) \end{matrix} \right] \\ \log\left|\det\frac{\partial y}{\partial x}\right| = \sum s(x_{1:d})$$
이뿐만 아니라 coupling 기반의 layer는 inverse도 쉽게 연산해낼 수 있다.
$$x_{1:d} = y_{1:d} \\ x_{d+1:D} = (y_{d+1:D} - t(y_{1:d})) \cdot \exp(-s(y_{1:d}))$$
1.1. Masked Convolution
RealNVP[3]에서는 partitioning을 binary mask를 통해 일반화 한다.
$$y = b \odot x + (1 - b) \odot \left( x \odot \exp(s(b \odot x)) + t(b \odot x) \right)$$
coupling layer 특성상 input의 일부에는 transform이 이뤄지지 않기 때문에, 연속된 coupling layer를 구성할 때는 binary mask를 alternating 하면서 모든 feature가 transform 될 수 있도록 구성한다.
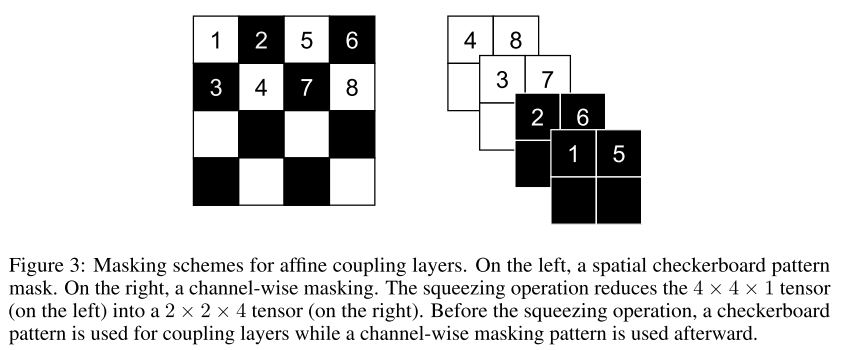
Figure 3: Masking schemes for affine coupling layers. (Dinh et al., 2017)
RealNVP[3]에서는 checkerboard pattern의 mask를 상정했으며 even index와 odd index를 번갈아 가며 trigging하는 방식으로 binary mask를 구성한다.
- Multi-scale architecture
RealNVP[3]는 input의 spatial size와 channel size 사이의 tradeoff를 위해 squeezing을 활용한다. 2x2xC의 subsquare를 1x1x4C로 squeezing 한다면 channel을 4배가량 늘릴 수 있게 된다.
RealNVP[3]는 multiple squeezing operation과 inter-coupling layer를 통해 여러 scale에서의 latent를 뽑고자 했다. 이때 전체 dimension이 유지되는 normalizing flow의 특성상 computational, memory cost는 고수준에서 유지되고, 부담을 줄이기 위해 각 scale에서 절반의 feature를 factorizing 한다.
$$h^{(0)} = x \\ (z^{i+1}, h^{i+1}) = f^{(i+1)}(h^{(i)}) \\ z^{(L)} = f^{(L)}(h^{(L-1)}) \\ z = (z^{(1)}, \ … , z^{(L)})$$
이 경우 latent z는 명시적으로 coarser scale의 정보와 finer scale의 정보를 분리하여 다룰 수 있게 된다. 이는 RealNVP[3]의 Appendix D.에서 확인 가능하다.
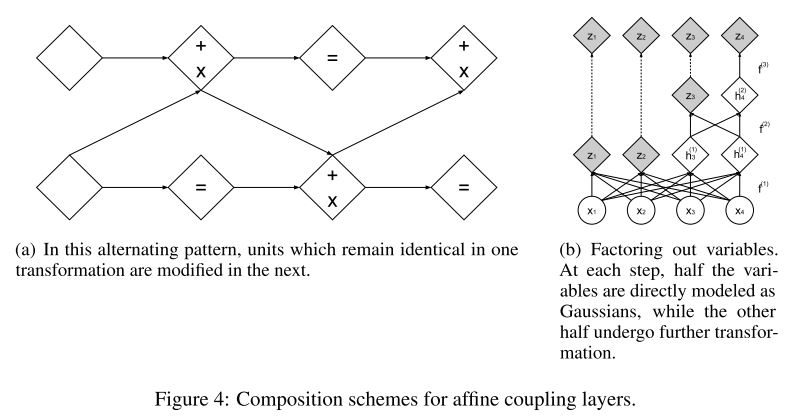
Figure 4: Composition schemes for affine coupling layers. (Dinh et al., 2017)
또한 intermediate representation을 직접 활용하기 때문에 gradient의 전달과 학습이 용이하다는 장점을 가진다.
- Batch normalization
training signal의 효율적인 전파를 위해 여러 모델은 batch normalization을 활용한다. RealNVP[3]에서는 running statistics를 활용하여 normalization을 구성한다.
$$x \mapsto \frac{x - \tilde \mu}{\sqrt{\tilde\sigma^2 + \epsilon}}$$
이 경우 linear rescaling과 동일하므로 jacobian은 $\sigma$의 곱으로 구성된다.
$$J = \left(\prod_i(\tilde\sigma^2 + \epsilon)\right)$$
Training, Sampling
이렇게 bijective를 활용한 invertible map $g: X \to Z$을 구성했다면, $x \in X$의 입력에 대해 forward pass로 latent $z = g(x) \in Z$를 구하고, 해당 latent를 통해 log-likelihood를 추정한다.
$$\log p_X(x) = \log p_Z(z) + \log\left|\frac{\partial g}{\partial x}\right|$$
원문에서는 prior $p(z)$를 gaussian으로 상정하였고, 추정된 log-likelihood를 maximize 하는 방식으로 네트워크를 학습시킨다.
sampling의 경우 prior에서 sampling한 noise $z \in Z$를 inverse pass하여 $x = g^{-1}(z) \in X$ 바로 사용할 수도 있고, 데이터로부터 latent를 구하여 interpolation 등 후처리 후 사용할 수도 있다.
$$z \sim p(z) \mapsto g^{-1}(z) \in X$$
Results
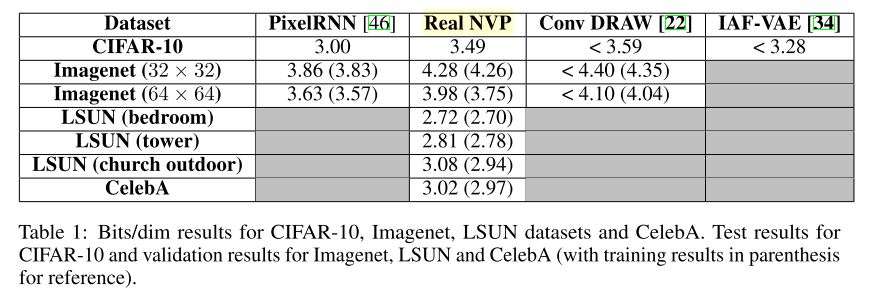
Table 1: Bits/dim results. (Dinh et al., 2017)

Figure 6: Manifold generated from four examples in the dataset. (Dinh et al., 2017)
Discusion
(사견)
Normalizing flow의 시작이 Rezende & Mohamed (2015)[1]는 아니었다. density estimation을 위해 Tabak & Vanden-Eijnden (2010)[4], Tabak & Turner (2013)[5]에서 제안이 되었고, 딥러닝을 활용한 probabilistic modeling으로 Rezende & Mohamed (2015)[1]에서 크게 유명해졌다.
비록 determinant와 inverse의 tractability로 인한 architectural constraint를 가지고 있지만, sampling이 single-forward pass로 가능하고, exact log-likelihood의 연산이 가능하다는 점에서 충분한 매력을 가진 모델이다.
추후 bijective에 대한 연구, VAE와의 상관성, 통합 가능성이 연구됨에 따라 더 많은 이야기가 남은 모델이므로 관심 가지고 봐도 좋을 것 같다.
Reference
[1] Rezende, D. J. and Mohamed, S. Variational inference with normalizing flows. In ICML 2015.
[2] Kingma, D. P. and Welling, M. Auto-encoding variational bayes. In ICLR 2014.
[3] Dinh, L., Sohl-Dickstein, J. and Bengio, S. Density estimation using Real NVP. In ICLR 2017.
[4] Tabak, E. G. and Vanden-Eijnden, E. Density estimation by dual ascent of the log-likelihood. Communications in Mathematical Sciences, 2010.
[5] Tabak, E. G. and Turner, C. V. A family of nonparametric density estimation algorithms. Communications on Pure and Applied Mathmatics, 2013.