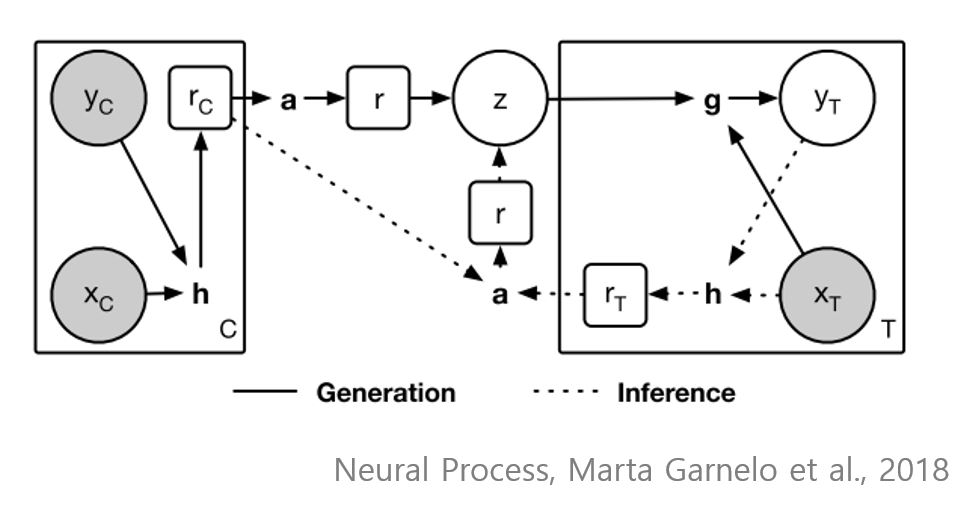
• Marta Garnelo et al., 2018, arXiv
• Keyword: Bayesian, Process
• Problem: Data inefficiency, hard to train multiple datasets in one.
• Solution: Stochastic Process + Latent variable + NN
• Benefits: Concurrent training, global uncertainty, explicit latent variable.
• Contribution: CNP + global uncertainty, concurrent dataset, explicit latent
• Weakness or Future work: Pairwise correlation.

Function Approximation

딥러닝에서는 데이터 간의 상관관계를 찾기 위해 함수를 근사하는 작업을 하는데, 주로 지도 학습에서는 parameterized function의 파라미터 셋을 gradient를 통해 업데이트하는 방식을 차용한다. 이러한 경우 대부분의 workload가 학습 중에 이뤄지며, 추론 과정은 단순 forward pass만으로 가능하다. 하지만 한번 학습된 이후로는 추론 결과의 업데이트가 힘들다는 점에서 메타 러닝 쪽도 관심이 많아지는 편이다.

그 대체재로 Stochastic Process와 그 에인 Gaussian Process(GP)가 있는데, 이러한 모델들은 training phase를 필요로 하지 않고, test-time에 원하는 쿼리를 직접 렌더링 하게 된다. 하지만 렌더링 과정이 O(N^3)의 연산이 필요하기 때문에 대형 데이터셋을 상대로 적용하기 쉽지 않고, kernel과 같은 prior에 의해 함수 모형이 바뀌는 등 여러 문제점도 존재한다.

이에 제안하고자 하는 게 Neural Process이다. 함수에 대한 분포를 가정하고, observation을 통해 query와 prediction에 대한 uncertainty를 추정한다. GP와 달리 O(n + m)의 단순 forward pass만으로 추정을 진행할 수 있다는 점에서 장점을 지닌다.

Neural Process

먼저 random function $F: \mathcal X \to \mathcal Y$와 finite seq $x_{1:n}=(x_1, …, x_n)$ with $x_i \in \mathcal X$, function values $Y_{1:n} := (F(x_1), …, F(x_n))$를 가정한다. 이 collection의 joint dist $\rho_{x_{1:n}}$이 존재할 것이고, GP 라면 multivariate gaussian일 것이다.

이 joint dist는 exchangeability와 consistentcy라는 조건에서 Kolmogorov Extension Theorem에 의해 stochastic process로 정의될 수 있다. 이 때 exchangeability는 permutation invariance를 의미하고, consistentcy는 marginlize한 범위 외의 sequence에 대해 marginalize했을 때 원본 시퀸스와 동일함을 의미한다.

Stochastic process F와 시퀸스 $x_{1:n}$, 그의 joint dist $\rho_{x_{1:n}}$에 대해 instantiation of stochastic process f는 다음과 같다

$$\rho_{x_{1:n}} = \int p(f)p(y_{1:n}|f, x_{1:n})df$$

observation noise를 고려하여 $Y_i \sim \mathcal N(f(x_i), \sigma^2)$라 가정하면 proability p는 다음과 같다

$$p(y_{1:n}|f, x_{1:n}) = \prod^{n}_{i=1} \mathcal N(y_i | f(x_i), \sigma^2)$$

이 때 joint dist $\lbrace\rho_{x_{1:n}}\rbrace$의 exchangeability와 consistentcy에 의해 stochastic process F의 존재성이 증명된다. 여기서 NP가 하고 싶은 것은 high-dimensional random vector z로 F를 parameterize하고, fixed function g에 대해 F(x) = g(x, z)를 NN으로 학습하고 싶은 것이다.

$$p(z, y_{1:n}|x_{1:n}) = p(z)\prod^{n}_{i=1} \mathcal N(y_i|g(x_i, z), \sigma^2)$$

이 때 random function과 distribution을 학습하기 위해서는 여러 데이터셋을 동시에 학습해야 한다. 여러 input seq $x_{1:n}$와 output seq $y_{1:n}$를 학습시켜 데이터 간의 variability를 학습할 수 있게 한다.

g를 non-linear NN으로 두기 때문에 학습에는 variational inference를 이용한다. latent z와 prior p(z)는 standard multivariate gaussian으로 두고, variational posterior $q(z|x_{1:n}, y_{1:n})$를 가정한다.

$$\log p(y_{1:n}|x_{1:n}) \ge \mathbb E_{q(z|x_{1:n}, y_{1:n})}\left[\sum^{n}_{i=1}\log p(y_i|z, x_i) + \log \frac{p(z)}{q(z|x _{1:n}, y _{1:n})}\right]$$

이 때 test time에 더욱 well-behave model을 만들기 위해 context-set과 target-set을 나누고, true posterior $p(z|x_{1:n}, y_{1:n})$ 대신 variational posterior로 approximate한다.

$$\log p(y_{1:n}|x_{1:n}) \ge \mathbb E_{q(z|x_{1:n}, y_{1:n})}\left[\sum^{n}_{i=m+1}\log p(y_i|z, x_i) + \log \frac{q(z|x _{1:m}, y _{1:m})}{q(z|x _{1:n}, y _{1:n})}\right]$$

이렇게 되면 z가 process F를 capture하는 역할을 하고, 이것이 global uncertainty를 capture 했다고도 볼 수 있다.

실제 구현체에서는 encoder h가 pair $(x, y)_i$에 대해 repr $r_i = h((x, y)_i)$로 구성하고, exchangeable aggregator $r = a(r_i) = \frac{1}{n} \sum^n _{i=1}r_i$를 통해 latent $z \sim \mathcal N(\mu(r), I\sigma(r))$를 표현한다. 마지막으로 decoder g와 sampled latent z에 대해 $y_T = g(z, x_T)$를 통해 output을 결정하게 된다.

z_context = self.z_encoder(context)
z_dist = self.z_prob(z_context)
latent = z_dist.sample()

rep = self.decoder(context, query, latent)
dist = self.normal_dist(rep)

log_prob = dist.log_prob(target)
log_prob = tf.reduce_sum(log_prob)

prior = self.z_prob(self.z_encoder(context))
posterior = self.z_prob(self.z_encoder([query, target]))

kl = tfp.distributions.kl_divergence(prior, posterior)
kl = tf.reduce_sum(kl)

elbo = -log_prob + kl

Conditional Neural Process, Marta Garnelo et al., 2018

동일 저자는 같은 해에 CNP라는 논문을 냈는데, 차이점은 NP는 latent z를 통해 process F를 캡처하고, global uncertainty를 측정하는데, CNP는 그러한 과정 없이 deterministic 하게 context와 query에 대한 target을 내놓는다. NP는 latent를 명시적으로 설정하였기 때문에, concurrent 한 training process에서도 명확히 latent를 포착하는 것을 볼 수 있다.

Discussion

NP는 역시 stochastic process와 NN을 합친 모델이다. 함수에 대한 분포를 정의하고, context conditioned prediction을 생성한다. regression task에 대해서 실험을 주로 했는데, future work로 high dimensional data에 관한 연구를 남겨두겠다 한다.

Implementation

• Tensorflow v1: tf-neural-process

Reference

• Conditional Neural Processes, Garnelo et al., 2018.
• Neural Processes, Garnelo et al., 2018.