Glow, Flow++

- Glow: Generative Flow with Invertible 1x1 Convolutions, Kingma and Dhariwal, 2018, arXiv
- Flow++: Improving Flow-Based Generative Models with Variational Dequantization and Architecture Design, Jonathan Ho et al., 2019, arXiv
- Keyword: Bayesian, Normalizing Flow, Glow, Flow++
- Problem: Inexpressiveness of engineered bijectives
- Solution: Invertible 1x1 convolution, variational dequantization, mixture of logistics
- Benefits: Lower bits/dim, better sample quality
- Weakness or Future work: -
Series: Normalizing flow
- Normalizing flow, Real NVP [link]
- Glow, Flow++ [this]
- ANF, VFlow [link]
- i-ResNet, CIF [link]
- SurVAE Flows [link]
Normalizing flow
latent variable model은 high-dimensional data로부터 내재된 패턴들을 축약한, 유의미한 latent space를 구성하고자 한다. 이는 주로 확률 모델로 구현되며, 크게 VAE, Flow와 같은 likelihood 기반의 모델과 GAN 부류의 모델로 구분할 수 있다.
Flow의 경우 데이터 $x \sim p_X^*(x)$에 대해 bijective sequence $\{f_k\}^L_{k=1}$를 통한 change of variables를 근간으로 한다. 자세한 정의는 이전 글을 따른다.
$$z = f_L \circ \ … \ \circ f_1(x) \\ \log p_X(x) = \log p_Z(z) + \sum^L_{k=1}\log\left|\det\frac{\partial f_k}{\partial f_{k-1}}\right| \ \ \mathrm{where} \ \ f_0 = x$$
transform에 bijective라는 constraint가 붙은 만큼 몇 가지 이점을 갖는다.
VAE의 경우 intractable posterior로 인해, variational inference를 통한 log-likelihood의 lower-bound 추정을 objective로 하지만, normalizing flow의 경우에는 change of variables를 통한 exact log-likelihood estimation과 inference가 가능하다.
또한 그 과정에서 encoder, decoder가 별개의 네트워크가 아닌, 파라미터를 공유하는 하나의 네트워크로 구성되므로 memory efficient 한 모델링이 가능하다.
이전 글에서 Rezende & Mohamed(2015)[1], RealNVP[2]로 물살을 탄 normalizing flow를 이번 글에서는 engineered bijective 관점에서 어떠한 발전이 있었는지 알아본다.
Glow
Glow[3]는 RealNVP[2]의 multi-scale architecture를 기반으로 더욱 풍부하고 다양한 engineered bijective를 하나의 flow block으로 구성한 모델이다.
기존의 RealNVP[2]가 Affine coupling, Batchnorm의 두 개 layer를 하나의 flow block으로 구성했다면, Glow는 ActNorm, Invertible 1x1 convolution, Affine coupling 3개 layer를 하나의 flow block으로 구성한다.
- ActNorm
RealNVP[2]에서는 deep models가 학습 중 겪게 되는 여러 문제를 해결하고자 batch normalization을 도입하였다. 하지만 batch norm의 경우 batch size에 영향을 받고, 그 크기가 작아짐에 따라 성능이 절감된다. 특히나 image의 경우 tensor size가 커 memory에 많은 양의 batch를 구성하지 못할 때에 치명적일 수 있다.
이에 Glow[3]에서는 activation normalization, 이하 actnorm을 제안한다. actnorm은 첫 번째 minibatch의 mean과 variance로 초기화한 parameter로 normalization을 진행한다. 이는 DDI(data-dependent initialization)을 따르고, 초기화된 이후에는 데이터와 독립된 일반적인 trainable parameter로 취급한다.
Batchnorm이 data에서 연산한 running statistics를 통해 normalization을 진행했다면, actnorm은 첫 번째 batch에서 연산한 statistics로 초기화한 파라미터를, 이후에는 데이터에 독립적인 trainable parameter로 상정하고 normalization을 진행한다는 점에서 차이가 존재한다.
물론 이렇게 학습된 parameter가 실제로 hidden state의 statistics를 따르지는 않는다.
$[h\times w \times c]$의 image tensor가 주어진다면, actnorm은 channel dimension에서 작동한다.
$$y \leftarrow \frac{x - \hat\mu}{\sqrt{\hat\sigma^2 + \epsilon}}, \ \ \log\left|\det\frac{\partial y}{\partial x}\right| = -h \cdot w \cdot\sum\log\sqrt{\sigma^2 + \epsilon}$$
- Invertible 1x1 convlution
RealNVP[2]와 같은 기성 모델은 coupling layer의 활용으로 인해 일부 channel에 identity map이 적용되었고, 모든 channel에 transform을 적용하기 위해 고정된 permutation operation을 활용하였다.
Glow[3]에서는 이 대체재로 invertible 1x1 convolution을 제안한다. invertible matrix를 근간으로 하는 linear projection은 어떤 basis로의 permutation으로 일반화되며, 1x1 conv는 이 과정에서 channel axis에 대한 일반화된 learnable permutation을 진행한다.
invertible 1x1 convolution의 log-determinant는 determinant of weight matrix로 귀결되며 다음과 같이 정리된다.
$$\log\left|\det\frac{d \mathrm{conv2D}(h; W)}{dh}\right| = h \cdot w \cdot \log\left|\det W\right|$$
문제는 weight matrix $W$의 determinant 연산은 $\mathcal O(c^3)$의 cubic 연산이기 때문에 channel의 크기가 커짐에 따라 intractable 하다는 특성을 가진다.
Glow[3]는 이를 위해 LU Decomposition을 제안한다. invertible matrix W를 두고, LDU factorized $L, D, U$를 trainable parameter로 가정한다. 그럼 non-zero diagonal matrix $D = \mathrm{diag}(s)$에 대해 다음과 같이 weight matrix W를 재구성할 수 있다. (이 때 permutation P는 고정이다.)
$$W = PL(U + \mathrm{diag}(s))$$
이에 log-determinant를 $\mathcal O(c)$의 linear time에 연산해낼 수 있게 된다.
$$\log\left|\det W\right| = \sum \log |s|$$
- Affine coupling
기존의 RealNVP[2]에서의 affine coupling에 몇 가지 trick을 제안한다.
우선 zero initialization이다. coupling layer는 affine transform에 활용할 파라미터를 NN을 통해 연산해내는데, 이때 NN 이후 추가 convolution을 하나 더 두고, 이의 weight을 0으로 두어 학습 초기에 identity function이 되도록 강제한다. 이것이 very dep networks의 학습에 도움을 주었다고 한다.
두 번째는 permutation에 관해서이다. Glow[3]는 invertible 1x1 convolution을 통해 permutation을 일반화하였으므로, RealNVP[2]와 같은 checkerboard pattern 형식의 mask가 큰 의미가 있지 않다. 따라서 Glow[3]에서는 단순히 절반의 channel을 split하고 concat하는 방식을 차용하였다고 한다.
Flow++
Flow++[4]의 저자는 Rezende & Mohamed, 2015[1], RealNVP[2], Glow[3]를 넘어선 여러 가지 normalizing flow에 관한 연구가 있었지만, 여전히 다른 generative model보다 표현력이 부족하다는 것을 느꼈다.
그는 그 문제점으로 3가지를 들었다.
1. uniform dequantization이 loss와 generalization의 suboptimal choice라는 것
2. affine coupling layer가 충분히 expressive 하지 않다는 것
3. coupling layer의 conditional network로 convolution은 충분히 powerful 하지 않다는 것
그리고 다음에서 그 대체재를 소개하고자 한다.
- Variational dequantization
이미지나 음성 데이터의 경우에는 continuous signal을 discrete representation으로 바꿔 저장하고, 이를 모델링하게 되는데, 단순히 continuous density model을 이에 fitting 하면, 대부분의 probability mass가 discrete point에 치중되며 품질이 떨어지는 현상이 발생한다.
이를 해결하기 위해 RNADE[5]에서는 dequantization을 제안했으며, 이는 uniform noise를 통해 data를 continous form으로 만들어 degenerate point로의 collapse를 방지하는 것이다.
$$P_\mathrm{model}(x) := \int_{[0, 1)^D}p_\mathrm{model}(x + u)du$$
또한 다음 전개에 의해서 dequantized data $y = x + u$의 log-likelihood를 discrete data $x$의 lower-bound로 볼 수 있다.
$$\mathbb E_{y \sim p_\mathrm{data}}[\log p_\mathrm{model}(y)] \\ = \sum_x P_\mathrm{data}(x) \int_{[0, 1)^D}\log p_\mathrm{model}(x+u)du \\ \le \sum_x P_\mathrm{data}(x)\log\int_{[0, 1)^D}p_\mathrm{model}(x+u)du \\ = \mathbb E_{x\sim P_\mathrm{data}}[\log P_\mathrm{model}(x)]$$
이를 통해 probability mass가 discrete point에 치중되고, degenerate mixture로 collapse 하는 현상을 막을 수 있었지만, 단순 unit hypercube $x + [0, 1)^D$로 모델링하기엔 uninformative 하고 unnatural 하다.
따라서 variational dequantization에서는 dequantization noise distribution을 variational $q(u|x)$로 상정하고 lower bound를 objective로 학습시킨다.
$$\mathbb E_{x\sim P_\mathrm{data}}[\log P_\mathrm{model}(x)] \\ = \mathbb E_{x\sim P_\mathrm{data}}\left[\log\int_{[0, 1)^D}q(u|x)\frac{p_\mathrm{model}(x+u)}{q(u|x)}du\right] \\ \ge \mathbb E_{x\sim P_\mathrm{data}}\left[\int_{[0, 1)^D}q(u|x)\log\frac{p_\mathrm{model}(x+u)}{q(u|x)}du\right] \\ = \mathbb E_{x\sim P_\mathrm{data}, \ u \sim q(\cdot|x)}\left[\log\frac{p_\mathrm{model}(x+u)}{q(u|x)}\right]$$
이때 variational distribution $q$는 flow-based model로 상정하여 $u = q_x(\epsilon), \ \mathrm{where} \ \epsilon \sim p(\epsilon) = \mathcal N(\epsilon; 0, I)$로 둔다. 이후 likelihood는 change of variables로 estimation이 가능하고 $q(u|x) = p(q_x^{-1}(u))\cdot|\partial q_x^{-1}/\partial u|$, lower bound objective는 다음과 같이 쓸 수 있다.
$$\mathbb E_{x \sim P_\mathrm{data}}[\log P_\mathrm{model}(x)] \le \mathbb E_{x \sim P_\mathrm{data}, \ \epsilon \sim p}\left[\log \frac{p_\mathrm{model}(x + q_x(\epsilon))}{p(\epsilon)\left|\partial q_x/\partial \epsilon\right|^{-1}}\right]$$
이에 발생하는 true likelihood와의 차는 $\mathbb E_{x\sim p_\mathrm{data}}[D_{KL}(q(u|x)||p_\mathrm{model}(u|x))]$이다. 이는 $q$를 uniform과 같은 inexpressive distribution을 상정했을 때 lower bound가 loose 해질 수 있음을 의미한다. 따라서 flow 기반의 $q$를 사용함으로써 더움 flexible 한 modeling이 가능하게 하였고, 실제로 train loss나 generalization에서 더 나은 성능을 보였다.
- Improved coupling layers
근래의 flow-based model은 대부분 affine coupling과 permutation layer을 활용했다. coupling layer의 경우 conditioning network $a_\theta, b_\theta$를 상정하여 입력 일부로부터 parameter를 설정, 이를 토대로 나머지 입력을 transform 한다.
$$y_1 = x_1, \ \ y_2 = x_2 \cdot \exp(a_\theta(x_1)) + b_\theta(x_1)$$
Flow++[4]의 저자들은 실험을 통해 더욱 expressive 한 coupling layer를 제안한다. 이는 mixture of logistics를 활용하여 invertible nonlinear transform을 가능케 한다.
$$x \mapsto \sigma^{-1}(\mathrm{MixLogCDF}(x;\pi, \mu, s)) \cdot \exp(a) + b \\ \mathrm{where} \ \ \mathrm{MixLogCDF}(x; \pi, \mu, s) := \sum^K_{k=1}\pi_i\sigma((x - \mu_i)\cdot\exp(-s_i))$$
이 때 $\{\pi_i, \mu_i, s_i\}_{i=1}^K, a, b$는 모두 neural network로 parameterizing한다.
- Expressive conditioning architectures with self-attention
기존까지는 coupling layer에서 conditioning network로 convolutional layer를 주로 상정했다면, 이번에는 multihead self-attention 기반의 network(Vaswani et al., 2017[6])를 활용해본다.
network는 stack of blocks로 구성되고, 각 block은 아래와 같이 구성된 뒤 residual connection과 layer normalization을 통해 연결된다.
$$\mathrm{Attn = Input \to Conv_{1x1} \to MultiHeadSelfAttention \to Gate}$$
이때 $\mathrm{Gate}$는 gated activation unit을 의미한다. network는 input tensor를 여러 개의 block에 forward하고, 마지막에 convolutional layer를 통해 coupling에 필요한 파라미터 수 만큼 channel을 늘리게 된다.
Experiments
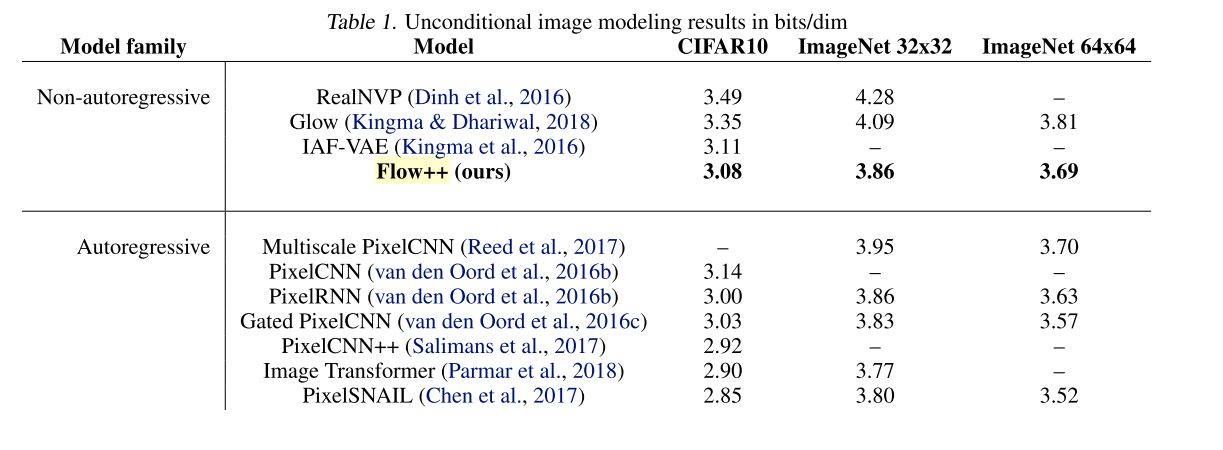
Table 1: Unconditional image modeling results in bits/dim. (Ho et al., 2019)
RealNVP[2], Glow[3], FlowW++[4]로 넘어오는 과정이 정량적으로 잘 나타났다.
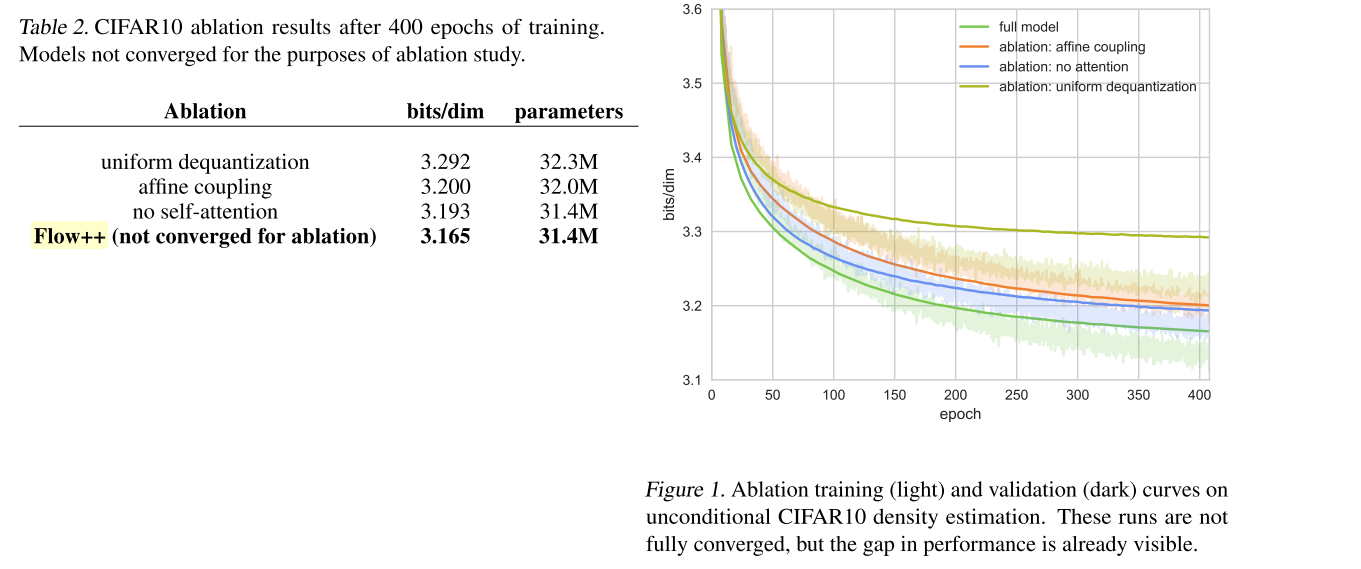
Table 2: CIFIAR10 ablation results after 400 epochs of training. (Ho et al., 2019)
또한 실제로 ablation study를 통해 component별 향상치도 확인할 수 있다.

Figure 6: Manipulation of attributes of a face. (Kingma & Dhariwal, 2018)
Discusion
(사견)
Flow는 bijective라는 constraint로 인해 기존의 nonlinearity를 근간으로 하는 expressiveness를 충분히 누리지 못했다. 그렇기 때문에 Flow 발전 초기에는 더욱 bijective block을 충분히 engineering 하여 표현력을 높이고자 하는 연구가 많았던 것 같다.
그 과정에서 actnorm, invertible 1x1 convolution, logistic coupler, variational dequantization 등 다양한 블럭이 나왔고, 이번 기회에 이를 소개하고자 했다.
이후에는 i-ResNet, ResFlow 등에서 residual network를 inversion 하는 시도 등을 통해 최대한 많은 feature에 nonlinearity를 활용하고자 하였고, 본격적으로 vae와의 통합을 위한 발판을 마련하기도 한다.
Reference
[1] Rezende, D. J. and Mohamed, S. Variational inference with normalizing flows. In ICML 2015.
[2] Dinh, L., Sohl-Dickstein, J. and Bengio, S. Density estimation using Real NVP. In ICLR 2017.
[3] Kingma, D. P. and Dhariwal, P. Glow: Generative Flow with Invertible 1x1 Convolutions. In NIPS 2018.
[4] Ho, J. et al. Flow++: Improving flow-based generative models with variational dequantization and architecture design. In ICML 2019.
[5] Uria, B., Murray, I. and Larochelle, Hugo. RNADE: The real-valued neural autoregressive density-estimator. In NeurIPS 2013.
[6] Vaswani, A. et al. Attention is all you need. In NeurIPS 2017.