Diffusion, WaveGrad and DiffWave
- Diffusion: Ho et al., 2020, arXiv:2006.11239
- WaveGrad: Nanxin Chen et al., 2020, arXiv:2009.00713
- DiffWave: Zhifeng Kong et al., 2020, arXiv:2009.09761
- Keyword: Denoising, Diffusion, Vocoder
- Problem: Quality and generation speed trade off on mel-inversion procedure.
- Solution: Denoising and diffusion based raw audio sampling.
- Benefits: Explicit trade off between speed and quality in single framework.
- Contribution: First use of denoising & diffusion model on vocoder, high fidelity audio generation, explicit trade off, etc.
- Weakness or Future work: -
Mel-inversion
Neural Text-to-Speech (TTS) 분야는 WaveNet(Oord et al., 2016), Char2Wav(Sotelo et al., 2017), Tacotron(Wang et al., 2017)을 거쳐 발전해 왔다. 그 중 Tacotron의 경우 text에서 mel-spectrogram을 예측하여 vocoder를 통해 raw-audio signal로 mel-inversion 하는 방식을 취한다.
현재는 많은 mel-inversion 모델들이 개발되었고, autoregressive 구조로 raw-audio와의 likelihood를 maximizing 하는 WaveNet(Oord et al., 2016), WaveRNN(Kalchbrenner et al., 2018), ExcitNet(Song et al., 2019a), LPCNet(Valin & Skoglund, 2019) 등의 모델이 있다.
하지만 이 경우 high sample rate를 가진 음성을 생성할 때 방대한 양의 frame 수에 비례하는 샘플링 시간을 가진다는 점에서 autoregressive의 근본적인 한계를 가지고 있었다.
이를 해결하고자 non-autoregressive vocoder의 연구가 활발해졌고, IAF를 기반으로 한 PWN(Oord et al., 2018), Glow를 기반으로 한 WaveGlow(Prenger et al., 2019), FloWaveNet(Kim et al., 2019), GAN을 기반으로 한 WaveGAN(Donahue et al., 2018), MelGAN(Kumar et al., 2019), PWG(Yamamoto et al., 2020), HooliGAN(McCarthy & Ahmed, 2020) 등이 발표되었다.
WaveGrad는 non-autoregressive vocoder 연구의 연속으로 raw signal의 log-density에서 gradient를 estimation 하는 방식으로 작동한다. 이를 통해 모델은 refinement step의 수를 조절함으로써 inference speed와 sample quality 사이의 trade off를 직접적으로 조절할 수 있게 되었고, autoregressive와 non-autoregressive 사이의 격차를 잇는 역할을 한다.
Denoising Diffusion Proabilistic Models, Jonathan Ho et al., 2020
WaveGrad와 DiffWave의 모델링은 기본적으로 Denoising Diffusion Model(Ho et al., 2020)을 따른다.

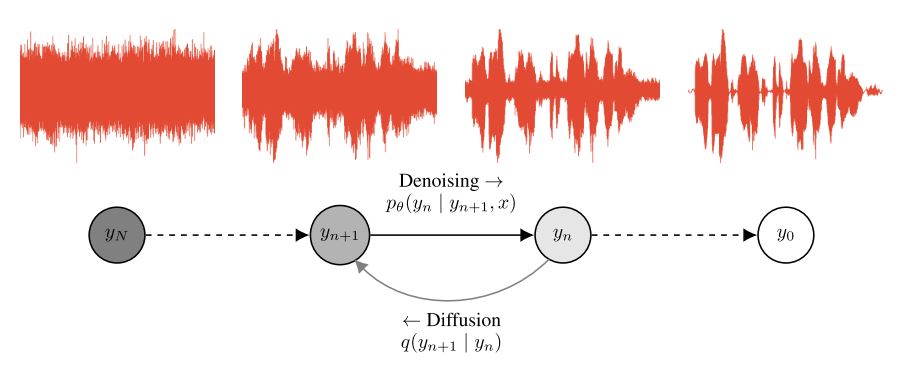
Figure 2: The directed graphical model considered in this work. (Ho et al., 2020)
Diffusion 모델은 finite step의 markov chain을 가정하여, 매 transition마다 sample에 noise를 더해간다. 이후 denoising을 위한 NN 모델을 두고 Diffusion의 reverse process를 학습하여 gaussian noise로부터 sample을 순차적으로 denoising하는 방식이다. 학습은 analytic 하게 구한 diffusion의 posterior와 denoising process 사이의 KL-divergence를 줄이는 방식으로 작동한다.
Formulation
Denoising model은 gaussian $p(\mathrm x_T) = \mathcal N(\mathrm x_T; 0, I)$을 시작으로, 동일한 dimension을 가지는 latent $\mathrm x_{T-1}, …, \mathrm x_{1}$을 거쳐 sample $\mathrm x_0 \sim q(\mathrm x_0)$로 향하는 latent variable model로 표현한다.
$$p_\theta(\mathrm x_0) := \int p_\theta(\mathrm x_{0:T})d\mathrm x_{1:T}$$
여기서 $p_\theta(\mathrm x_{0:T})$를 reverse process라 정의하고, markov chain으로 모델링하면 다음과 같다.
$$p_\theta(\mathrm x_{0:T}) := p(\mathrm x_T)\prod^T_{t=1}p_\theta(\mathrm x_{t-1}|\mathrm x_t)$$
$$p_\theta(\mathrm x_{t-1}|\mathrm x_t) := \mathcal N(\mathrm x_{t-1}; \mu_\theta(\mathrm x_t; t), \Sigma_\theta(\mathrm x_t; t))$$
denoising, diffusion 모델이 다른 latent variable model과 다른 점은, diffusion process를 analytic 하게 정의하여 posterior를 직접 approximate 한다는 것이다. End-to-End로 full transition을 학습하는 것이 아닌, state에 직접적인 constraint를 가한다.
Ho et al., 2020. 에서는 diffusion process를 모델에 noise를 더하는 markov chain으로 정의하고, 더해질 noise의 variance를 scheduler sequence $\beta_1, …, \beta_T$로 두어 다음과 같이 정의한다.
$$q(\mathrm x_{1:T}|\mathrm x_0) := \prod^T_{t=1}q(\mathrm x_t|\mathrm x_{t-1})$$
$$q(\mathrm x_t | \mathrm x_{t-1}) := \mathcal N(\mathrm x_t; \sqrt{1 - \beta_t}\mathrm x_{t-1}, \beta_t \mathrm I)$$
이는 autoregressive하게 정의하는 대신, $\mathrm x_0$에 직접 condition 하는 방식으로 표현할 수 있다.
$$q(\mathrm x_t|\mathrm x_0) = \mathcal N(\mathrm x_t; \sqrt{\bar \alpha_t}\mathrm x_0, (1 - \bar \alpha_t)\mathrm I) \\ \mathrm{where}\ \alpha_t = 1 - \beta_t, \ \bar\alpha_t = \prod^t_{s=1}\alpha_t$$
이렇게 되면 nll에 대한 variational lower bound는 state 사이의 KL-divergence로 rewriting할 수 있다.
$\mathbb E[-\log p_\theta(\mathrm x_0)] \\ \le \mathbb E_q\left[-\log \frac{p_\theta(\mathrm x_{0:T})}{q(\mathrm x_{1:T}|\mathrm x_0)}\right] \\= \mathbb E_q\left[ -\log p(\mathrm x_T) - \sum_{t\ge 1} \log\frac{p_\theta(\mathrm x_{t-1}|\mathrm x_t)}{q(\mathrm x_t|\mathrm x_{t-1})} \right] \\= \mathbb E_q\left[ -\log p(\mathrm x_T) - \sum_{t\ge 1} \log\frac{p_\theta(\mathrm x_{t-1}|\mathrm x_t)}{q(\mathrm x_{t-1}|x_t)} \cdot \frac{q(\mathrm x_{t-1})}{q(\mathrm x_t)} \right] \\=\mathbb E_q\left[ -\log\frac{p(\mathrm x_T)}{q(\mathrm x_T)} - \sum_{t\ge 1} \log \frac{p_\theta(\mathrm x_{t-1}|\mathrm x_t)}{q(\mathrm x_{t-1}|\mathrm x_t)} - \log q(\mathrm x_0) \right] \\=D_{\mathrm{KL}}(q(\mathrm x_T)||p(\mathrm x_T)) + \mathbb \sum_{t\ge 1} D_\mathrm{KL}(q(\mathrm x_{t-1}|\mathrm x_t)||p_\theta(\mathrm x_{t-1}|\mathrm x_t)) + H(\mathrm x_0)$
이 때 $q(\mathrm x_{t-1}|\mathrm x_t, \mathrm x_0)$의 analytic form은 다음과 같다.
$$q(\mathrm x_{t-1}|\mathrm x_t, \mathrm x_0) = \frac{q(\mathrm x_t|\mathrm x_{t-1})q(\mathrm x_{t-1}|\mathrm x_0)}{q(\mathrm x_t|\mathrm x_0)} = \mathcal N(\mathrm x_{t-1}; \tilde \mu_t(\mathrm x_t, \mathrm x_0), \tilde \beta_t \mathrm I) \\ \mathrm{where} \ \tilde\mu_t(\mathrm x_t, \mathrm x_0) := \frac{\sqrt{\bar a_{t-1}}\beta_t}{1 - \bar a_t}\mathrm x_0 + \frac{\sqrt{\alpha_t}(1 - \bar\alpha_{t-1})}{1 - \bar\alpha_t}\mathrm x_t \ \ \mathrm{and} \ \ \tilde\beta_t := \frac{1 - \bar\alpha_{t-1}}{1 - \bar\alpha_t}\beta_t$$
Reparametrization
각각의 Dkl term을 순서대로 $L_T, L_{1:T-1}, L_0$로 정의하면, $L_T$는 beta를 learnable 하지 않은 constant로 가정할 때 상수로 고정되기 때문에 연산에서 제외한다.
$L_{1:T-1}$은 $\Sigma_\theta(\mathrm x_t, t) = \sigma^2_t\mathrm I$의 경우 untrained constants로 제외하고, $\mu_t$에 대해서만 학습을 진행한다. $\sigma_t$는 $\sigma_t^2 = \beta_t$나 $\sigma^2_t = \tilde\beta_t = \frac{1 - \bar\alpha_{t-1}}{1 - \bar\alpha_t}\beta_t$로 실험적으로 설정하였다. 이는 data에 대한 reverse process entropy의 upper, lower bound라고 한다.
$\mu_\theta(x_t, t)$는 KL에서 trainable term을 구축한다.
$$L_{t-1} = \mathbb E_q\left[ \frac{1}{2\sigma^2_t}||\tilde\mu_t(\mathrm x_t, \mathrm x_0) - \mu_\theta(\mathrm x_t, t)||^2 \right] + C$$
이를 previous term을 통해 다시 써보면 다음과 같다.
$L_{t-1} - C \\=\mathbb E_q\left[ \frac{1}{2\sigma^2_t} \left|\left| \frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1 - \bar\alpha_t}\mathrm x_0 + \frac{\sqrt{\alpha_t}(1 - \bar\alpha_{t-1})}{1 - \bar\alpha_t}\mathrm x_t - \mu_\theta(\mathrm x_t, t) \right|\right|^2 \right] \\=\mathbb E_q\left[ \frac{1}{2\sigma^2_t} \left|\left| \frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1 - \bar\alpha_t}\frac{1}{\sqrt{\bar\alpha_t}}(x_t - \sqrt{1 - \bar\alpha_t}\epsilon) + \frac{\sqrt\alpha_t(1 - \bar\alpha_{t-1})}{1 - \bar\alpha_t}x_t - \mu_\theta(x_t, t) \right|\right|^2 \right] \\=\mathbb E_q\left[ \frac{1}{2\sigma^2_t} \left|\left| \frac{1}{\sqrt{\alpha_t}}\left( \frac{\beta_t + \alpha_t(1 - \bar\alpha_{t-1})}{1 - \bar\alpha_t}x_t - \frac{\beta_t}{\sqrt{1 - \bar\alpha_t}}\epsilon \right) - \mu_\theta(x_t, t) \right|\right|^2 \right] \\=\mathbb E_q\left[ \frac{1}{2\sigma^2_t} \left|\left| \frac{1}{\sqrt{\alpha_t}}\left( x_t - \frac{\beta_t}{\sqrt{1 - \bar\alpha_t}}\epsilon \right) - \mu_\theta(x_t, t)\right|\right|^2 \right] \\\mathrm{where} \ \ \mathrm x_t = \sqrt{\bar\alpha_t}\mathrm x_0 + \sqrt{1 - \bar\alpha_t}\epsilon$
위 정리에서 $\mu_\theta$는 $\epsilon_\theta$를 통해 reparametrizing 할 수 있다.
$$\mu_\theta(\mathrm x_t, t) = \frac{1}{\sqrt\alpha_t}\left( \mathrm x_t - \frac{\beta_t}{\sqrt{1 - \bar\alpha_t}}\epsilon_\theta(\mathrm x_t, t) \right) \\\mathbb E_{\mathrm x_0, \epsilon}\left[ \frac{\beta^2_t}{2\sigma^2_t\alpha_t(1 - \bar\alpha_t)}||\epsilon - \epsilon_\theta(\sqrt{\bar\alpha_t}\mathrm x_0 + \sqrt{1 - \bar\alpha_t}\epsilon, t)||^2 \right]$$
최종 objective는 scale term을 생략한 weighted variational bound로 나타낸다.
$$L_\mathrm{simple}(\theta) := \mathbb E_{t, \mathrm x_0, \epsilon}\left[ || \epsilon - \epsilon_\theta(\sqrt{\bar\alpha_t}\mathrm x_0 + \sqrt{1 - \bar\alpha_t}\epsilon, t)||^2\right]$$
원문에서는 실제로 이렇게 formulation 된 objective가 성능이 더 좋았음을 실험으로 보였다.
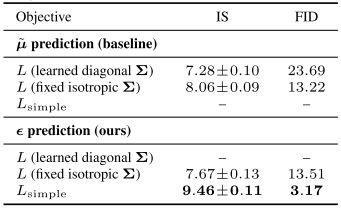
Table 2: Unconditional CIFAR10 reverse process parameterization and training objective ablation. (Ho et al., 2020)
정리하면 $L_\mathrm{simple}$은 두 process 사이의 Kl-divergence를 재구성한 것이고, 이는 single NN을 통해 현재 input에 존재하는 noise를 noise-level에 따라 직접 예측하여 denoising하는 방식으로 다음 state로의 transition을 진행한다.

Algorithms from Ho et al., 2020.
따라서 state의 수가 늘어나면 더 정교하고, 더 많은 noise를 제거하여 sample quality를 높일 수 있지만 sampling 시간이 길어지고, state 수가 줄어들면 sample에 noise가 낄 수 있지만 이른 시간 안에 결과를 얻을 수 있다.
WaveGrad: Estimating Gradients for WaveForm Generation, Nanxin Chen et al., 2020.
WaveGrad는 위 formulation을 통해서 mel-spectrogram에 condition 한 raw signal을 생성하는 방법론을 제시한다.
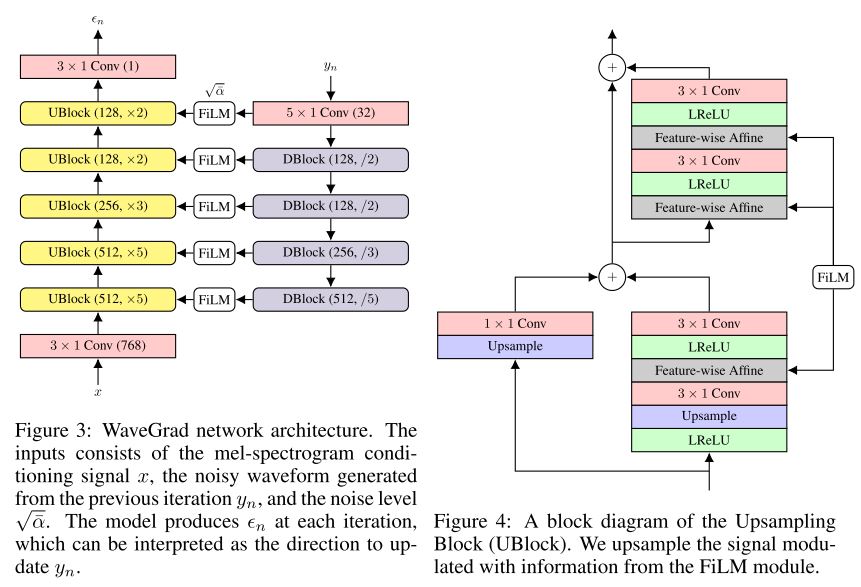
Figure 3, 4: WaveGrad network architecture, upsampling block.
Downsampling block(DBlock)에서 noised signal의 feature를 추출하고, Upsampling block(UBlock)에 feature과 mel-spectrogram을 입력으로 주어 noise를 예측한다.
원문에서는 24kHz의 raw audio에서 80Hz의 mel을 연산하여, mel-frame 하나당 300개의 audio frame으로 확장하는데, 이는 5개의 UBlock에서 각각 [5, 5, 3, 2, 2] factor에 맞게 upsampling하는 방식으로 구성하고, DBlock에서는 반대로 noised signal을 [2, 2, 3, 5]로 downsampling하여 각각의 intermediate representation의 resolution을 matching 할 수 있도록 두었다.
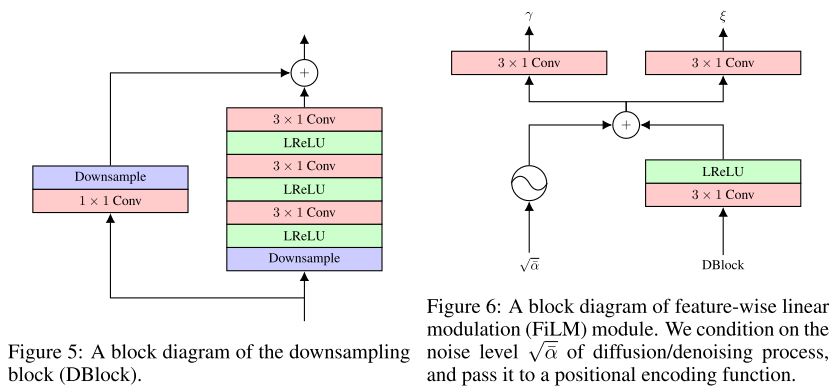
Figure 5, 6: Block diagrams of the downsampling, feature-wise linear modulation (FiLM) blocks.
각각의 convolution은 receptive field를 넓히기 위해서 dilation factor를 가지고, UBlock의 4개 conv는 [1, 2, 1, 2]와 [1, 2, 4, 8], DBlock의 3개 conv는 [1, 2, 4]로 구성된다.
upsample과 downsample 과정에 정보전달을 위해 wavegrad에서는 Feature-wise linear modulation (FiLM)모델을 통해 noise-level과 positional encoding, DBlock의 feature를 affine parameter로 바꿔 UBlock에서 feature-wise affine transform을 진행한다.
이외에 batch normalization의 경우 batch에 여러 개의 noise-level을 가진 sample 들이 존재하기 때문에 batch statistics가 정확하지 않아 sample quality에 악영향을 미쳤다고 한다.
Noise Scheduling

objective를 구성하기 위해서는 noise level $\sqrt{\bar\alpha_t}$에 대한 설정이 필요하다. learnable한 parameter로 둘 것이 아니므로 noise distribution에 직접 영향을 줄 수 있어 sample quality와 긴밀한 연관성을 가진다. WaveGrad에서는 noise level에 대한 설정이 음질과 직접적인 연관이 있었음을 실험으로 보였다.

Figure 7: A plot of different noise schedules
원문에서는 iteration의 수에 따라 noise level scheduling method를 따로 두었는데, 1000회의 경우 $\beta_t$를 1e-4에서 0.005를 linear 하게 1000개, 50의 경우 1e-4에서 0.05를 linear 하게 50개 sample 하였다. 25회의 경우에는 $\beta_0 = 1\times 10^{-6}, \ \beta_1 = 2\times 10^{-6}$을 시작으로 하는 fibonacci sequence를 구축하였고, 6회의 경우에는 manual 하게 [1e-6, 1e-5, .., 1e-1]로 exponential scale에서 linear 하게 구현하였다.
이후 이를 통해 partition $l_0 = 1, \ l_s = \sqrt{\prod^s_{i=1}(1 - \beta_s)}$을 설정하고, $(l_{s-1}, l_s)$에서 uniform 하게 $\sqrt{\bar\alpha}$를 sampling 하여 사용한다. 이렇게 되면 discrete index가 아닌 continuous segment에서 noise level을 sampling 할 수 있고, 6iter과 같이 sparse 한 scheduling 수준에서 괜찮은 성능을 보였다고 한다.
Experiments, Discussion
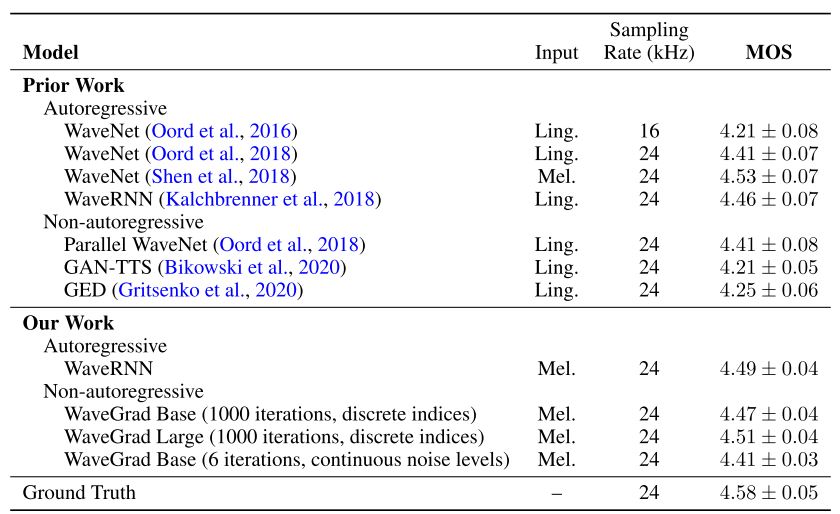
Table 1: Mean opinion scores (MOS) of various models and their confidence intervals.
원문에서는 이 외에도 iteration 수를 줄이기 위해 여러 가지 noise schedule을 시도했으며, 잘 작동하는 schedule은 $D_\mathrm{KL}(q(y_N|y_0)||\mathcal N(0, I))$을 작게 두어 train-inference의 격차가 거의 없게 두었고, $\beta$를 작은 값으로 시작하여 fine granuality details에 따라 background noise를 줄여야 했다고 한다.
DiffWave: A Versatile Diffusion Model for Audio Synthesis, Zhifeng Kong et al., 2020
(2020.09.24. update)
DiffWave는 WaveGrad와 같은 시기에 나온 또 다른 Diffusion denoising 기반의 mel-inversion vocoder이다.
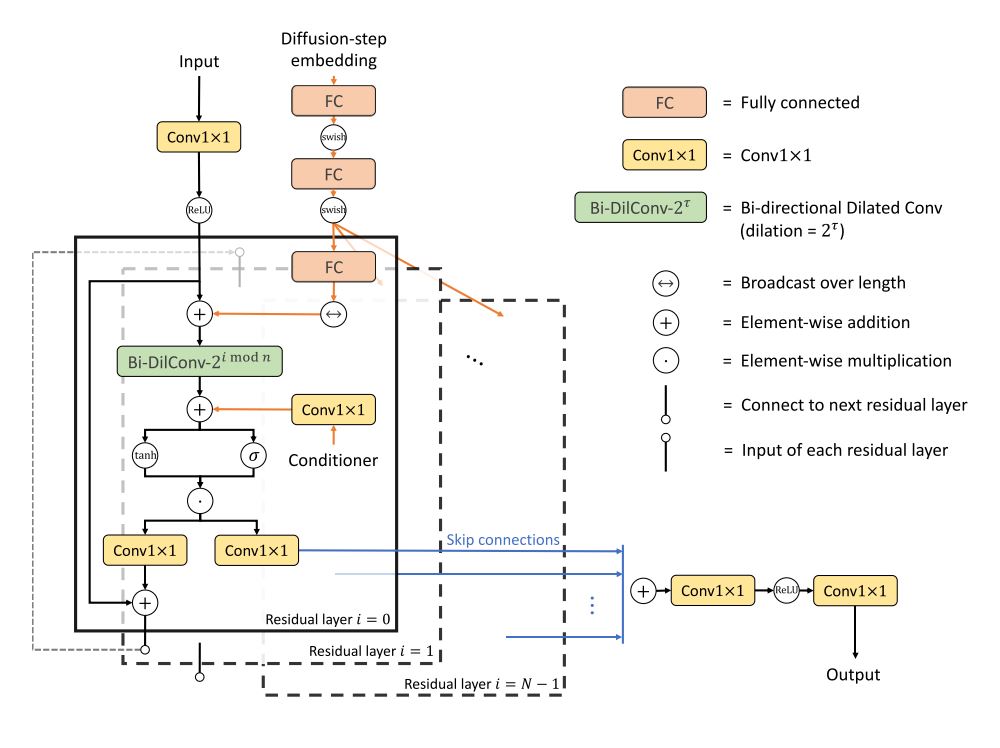
Figure 2: The network architecture of DiffWave
DiffWave는 기본적으로 WaveNet 아키텍쳐를 차용한다. kernel-size=3과 dilation-factor=2의 기본적인 noncausal dilated convolution을 기반으로 [1, 2, …, 512]의 10개 레이어를 3개 cycle로 구성한다.
Noise schedule에 대한 embedding을 $\sqrt{\bar\alpha}$에 직접 condition 하던 WaveGrad와 달리 DiffWave에서는 timestep을 기반으로 한 modified positional encoding에 FC-swish layer를 덧붙여 활용한다.
$$t_\mathrm{embedding} = \left[ \sin(10^{\frac{0\times 4}{63}}t), \cdot\cdot\cdot, \sin(10^{\frac{63\times 4}{63}}t), \cos(10^{\frac{0\times 4}{63}}t), \cdot\cdot\cdot, \cos(10^{\frac{63\times 4}{63}}t) \right]$$
mel-spectrogram은 channel이 1개인 2D tensor로 가정하여 2D transposed convolution에 의해 22kHz의 signal resolution으로 upsample 되고, WaveNet block에서 dilated convolution 이후에 bias term으로 더해진다.
noise scheduling의 경우 [20, 40, 50] iteration에서 $\beta_t$를 [1e-4, 0.02]를 linear sampling, 200 iteration의 경우 [1e-4, 0.05]를 linear sampling 하였다고 한다.
DiffWave는 특이하게도 Vocoder purpose 외에 unconditional generation을 시도하였다. 이 경우 보통의 wavenet이라면 single model이 음성의 길이를 모두 커버할 수 있는 receptive field를 구축해야 하지만, DiffWave의 경우 denoising 과정에 발생하는 iteration으로 이에 비례하는 추가 receptive field를 쉽게 얻을 수 있었다.
Experiments, Discussion
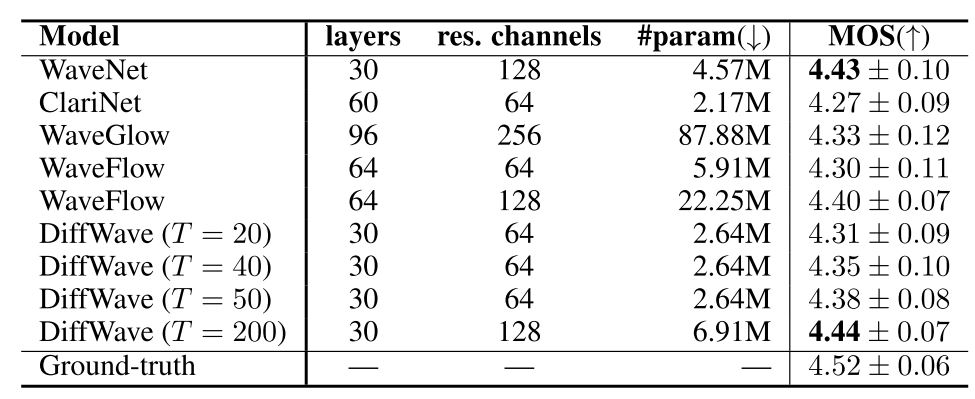
Table 1: The model hyperparameters, model foot print, and 5-scale MOS with 95% confidence intervals
Vocoder task의 경우 DiffWave는 다른 Flow-based SOTA 모델보다는 조금 느리지만, sample quality는 더 좋았다고 한다. 이는 Flow-based Model이 가지는 architectural constraint에 의한 것으로 추측하였고, inference 속도는 추가 engineering에 의해 일정 부분 빨라질 수 있을 것으로 보인다.
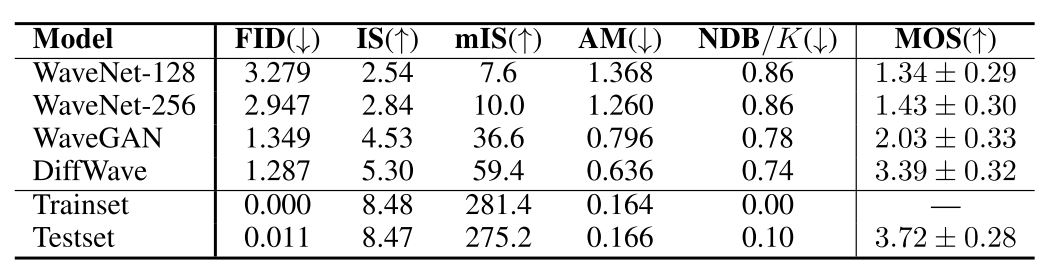
Table 2: The automatic evaluation metrics and 5-scale MOS with 95% confidence intervals.
Unconditional generation task의 경우에는 Speech Commands Dataset 에서 spoken digits (0~9) 부분만을 발췌하여 사용했다고 한다. 길이는 16kHz의 1초 미만으로 활용하여 여러 가지 evaluation metric을 측정하였다.
Implementation
- official, Jonathan Ho, tf: diffusion
- official sample: wavegrad.github.io
- unofficial, Ivan Vovk, pytorch: WaveGrad
- official sample: diffwave-demo.github.io
- unofficial, revsic, tensorflow2: tf-diffwave
Reference
- WaveNet: A Generative Model for Raw Audio, Oord et al., 2016.
- Char2Wav: End-to-End Speech Synthesis, Sotelo et al., 2017.
- Tacotron: Towards End-to-End Speech Synthesis, Wang et al., 2017.
- WaveRNN: Efficient Neural Audio Synthesis, Kalchbrenner et al., 2018.
- ExcitNet Vocoder: A Neural Excitation Model for Parametric Speech Synthesis, Song et al., 2019a.
- LPCNet: Improving Neural Speech Synthesis through Linear Prediction, Valin & Skoglund, 2019.
- Parallel WaveNet: Fast High-Fidelity Speech Synthesis, Oord et al., 2018.
- WaveGlow: A Flow-based Generative Network for Speech Synthesis, Prenger et al., 2019.
- FloWaveNet: A generative flow for raw audio, Kim et al., 2019.
- WaveGAN: Adversarial Audio Synthesis, Donahue et al., 2018.
- MelGAN: Generative Adversarial Networks for Conditional Waveform Synthesis, Kumar et al., 2019.
- Parallel WaveGAN: A Fast Waveform Generation Model based on Generative Adversarial Networks, Yamamoto et al., 2020.
- HooliGAN: Robust, High Quality Neural Vocoding, McCarthy & Ahmed, 2020.
- Denoising Diffusion Proabilistic Models, Ho et al., 2020.