아래 글은 비공식적인 개인의 사견임을 밝힌다.

• Essay of generative models, Mode coverage
• Keyword: Excplicit, Implicit modeling, Contrastive learning

Introduction

근래의 Generative Models는 VAE[arXiv:2112.07804], Normalizing Flow[arXiv:1807.03039], Diffusion[arXiv:2006.11239], GAN[arXiv:1812.04948] 등의 프레임워크에 따라 학습된다.

이들은 데이터의 분포를 학습하여, 데이터 포인트를 샘플링하기 위한 목적으로 학습 방식을 구성한다.

생성 모델은 크게 2개 부류로 볼 수 있다.

• Likelihood-based Model: VAE, Flow, Diffusion 등 생성된 샘플에 대해 우도 함수를 최대화하는 방식
• Implicit Model: GAN 등 Divergence와 같은 부차적 방식을 통해 분포를 학습하는 방식

이중 Normalizing flow만이 유일하게 invertible operations와 change of variables를 통해 exact likelihood의 추정이 가능하고,
VAE와 Diffusion은 likelihood의 lower bound를 최대화하는 방식을 취한다.

Likelihood를 기반으로 한 모델을 explicit 모델이라고 표현하기도 하고, 그 외 요소를 활용한 경우를 implicit 모델이라고 하는 듯 하다.

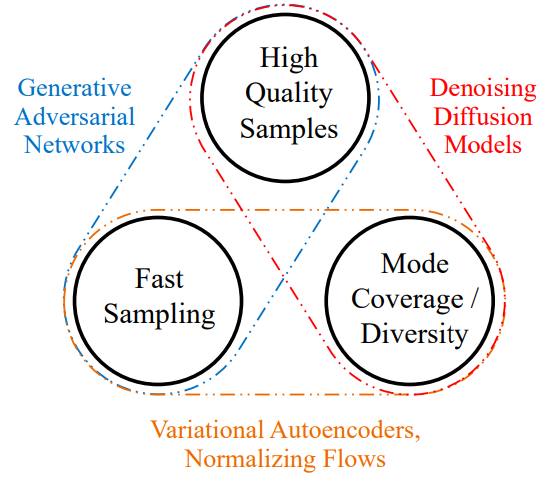
[arXiv:2112.07804]에서는 생성 모델의 특성 3가지를 통해 이들을 분류한다.

• GAN은 빠른 합성과 Sharp한 샘플링이 가능하지만, 고질적으로 Modal collapse를 포함하고
• VAE와 Flow는 빠른 샘플링과 높은 Mode coverage를 보이지만, 데이터 샘플이 Smooth한 편이다.
• Diffusion은 Mode coverage, sharp sampling이 모두 가능하지만, 실시간 합성이 어렵다.

이를 Generative trilemma라고 일컬었으며, 이를 개선하기 위해 최근 여러 가지 시도들이 이뤄지고 있다.

이 중 오늘 이야기 다뤄보고자 하는 것은 Mode coverage이다.

Why Modal collapse occurs on GAN

GAN의 가장 흔한 설명은 경찰과 도둑의 이야기이다.

Generator가 데이터 샘플을 생성하면, Discriminator는 주어진 샘플이 합성된 것인지, 자연적으로 발생한 것인지 검측한다. Generator는 Discriminator가 합성 샘플을 자연 샘플로 여기도록 학습하고, Discriminator는 Generator의 샘플을 분류하도록 학습된다.

$$\min_G\max_D \mathbb E_{x\sim p_\mathrm{data}(x), z\sim p(z)}[\log D(x) + \log (1 - D(G(z)))]$$

다양한 GAN 모델은 Generator 1번, Discriminator 1번을 교차하며 학습하는 방식의 프레임워크를 선택했다.

이 과정에서 Generator는 $x_\ast = \arg\max_x \log(D(x))$를 생성하는 single point generator가 될 수도 있고, Discriminator는 해당 single point만 분간하면 되는 단순한 모델이 될 수도 있다.

Generator가 샘플 전반의 Modal을 커버하지 않더라도, 이를 penalize 할 제약이 없기에, 여러 엔지니어링을 통해 Modal collapse를 완화할 수는 있지만, 근본적으로 해결하기란 쉽지 않다.

반면 Likelihood-based 모델은 다르다.

VAE, Diffusion의 경우 posterior $z \sim q(x)$을 두고 $p(x|z)$의 conditional generation에 대한 likelihood를 취한다. 이 과정에서 데이터 포인트의 복원이란 제약이 발생하고, 모델은 Modality를 모두 커버하는 시도가 발생하게 된다.

Flow의 경우 invertible operation을 통해 exact posterior $z = f(x)$와 conditional generation $x = f^{-1}(z)$를 보장받고, $p_z(f(x))$를 maximize 하는 것만으로 데이터 포인트의 관찰이 이뤄진다.

현대의 3개 생성 프레임워크 중 GAN 프레임워크만이 데이터 포인트의 관찰과 커버에 대한 제약이 존재하지 않는 것이다.

이번 글에서는 Likelihood-based 모델의 posterior encoder, sample generator 2개 관점에서의 collapse 해결법을 GAN에서는 어떻게 활용해야 할지 이야기해본다. 그리고 KL-Divergence, Contrastive learning, Generator Diversity Loss가 어떻게 연결될 수 있을지의 직관을 공유한다.

KL-Divergence

$$\mathbb E_{x\sim p_\mathrm{data}(x)}[\log p(x|q(x)) + \log p(q(x))]$$

고전 Autoencoder는 반대로 posterior의 diversity에 대한 constraint가 없었다. posterior distribution $z\sim q(\cdot|x)$에서 collapse가 발생할 수 있었고, prior에서 sampling을 하면 decoder 입장에서는 unseen point가 들어오는 것이 된다.

$$\mathbb E_{x\sim p_\mathrm{data}(x), z\sim q(z|x)}[\log p(x|z) + \log \frac{p(z)}{q(z|x)}]$$

VAE[arXiv:1312.6114]에서는 posterior의 sampling과 entropy을 활용한다.

concrete point가 아닌 stochastic point를 활용하고, entropy term이 posterior collapse를 방지하는 regularizer로 작용한다.

실제로 코드 수준에서 보면 entropy term은 $\mu, \sigma^2 = q(\cdot|x)$ 에서 $\sigma$를 최대화하는 방식으로 작동한다. encoder는 최대한 prior 내에서 작동하게 하고, decoder가 가능한 prior의 다양한 샘플 포인트를 보도록 구성한 것이다.

Posterior approximator in GAN

이는 AE에서의 문제만은 아니다.

현대의 다양한 생성 모델은 unseen context의 generalization을 위해 embedding 보다 네트워크 기반의 information encoder를 사용하는 편이다.

StarGAN 같이 style code를 생성하는, 일종의 posterior encoder를 가진 아키텍처가 있다고 가정하자. posterior encoder에서 collapse가 발생한다면, generator에서는 generalization 문제와 연쇄적인 modal collapse로 발전할 수 있다.

GAN이라도 Information encoder를 가진 아키텍처라면, posterior collapse 방지를 위한 regularizer를 고려해볼 법하다.

Contrastive and Diversity loss

posterior collapse는 entropy term을 활용한 regularization으로 해결하였다.
그렇다면 generator modal collapse는 어떻게 해결해야 할까

2020년 전후로 Contrastive learning은 어느덧 representation learning의 메인 테마로 자리매김하였다. 비전에서는 SimCLR[arXiv:2002.05709], 음성에서는 Wav2Vec2.0[arXiv:2006.11477] 등의 representation들이 공개되었다.

$$I(x_{t+k}, c_t) \ge \log N + \mathbb E_{\mathcal X}\left[\log\frac{f_k(x_{t + k}, c_t)}{\sum_{x_j \in \mathcal X}f_k(x_j, c_t)}\right]$$

Contrastive learning의 major contribution은 기존까지 positive case에 대해서만 objective를 취하던 방식과 달리 negative case, contrastive case에 대해 objective를 취해 representation 사이의 mutual information을 최대화한다는 것이다. [arXiv:1807.03748]

기존까지의 representation learning에서도 collapse 현상은 발생하고 있었고, 이를 negative case에 대한 penalizing으로 해결한 것이다. 그렇다면, 생성 모델에서도 negative case에 대한 penalizing이 이뤄진다면, modal collapse가 완화될 수 있을 듯 하다.

가장 먼저 정의할 것은, 생성 모델에서 하나의 데이텀 포인트가 생성되면, 해당 샘플의 negative case가 무엇인가이다.

만약 latent space의 크기가 데이터 공간의 크기보다 작거나 같다면, 모든 데이텀 포인트를 커버하기 위해 generator는 injective, 일대일 함수여야 한다. 이는 두 잠재 변수가 다르다면, 생성되는 두 결과물이 달라야 함을 의미한다.

우리에게 negative case는 generator가 injective일 때, 다른 latent에서 생성되는 결과물이 같은 경우로 정의할 수 있을 것이다.

$$\mathbb E_{\mathcal Z}[-\log\sum_{z_j \in \mathcal Z} f(G(z_j), G(z))]$$

만약 샘플 포인트를 Laplacian으로 가정하면, $\sum_{z_j \in \mathcal Z}||G(z_j) - G(z)||_1$로 표현할 수 있고, 이는 StarGAN.v2[arXiv:1912.01865]의 diversity loss에 대응한다.

이에 GAN의 diversity loss는 Generator가 injective일 때 negative case에 대한 contrastive loss로 해석할 수도 있게 된다. 그리고 modal collapse의 완화를 위한 regularizer로 이해할 수 있다.

Wrap up

Posterior collapse, representation collapse의 해결은 대체로 entropy term, negative case penalizer을 포함하는 방식으로 해결하였다.

처음으로 돌아가 Likelihood-based model은 1) 데이터 포인트의 직접 관찰과 2) 커버 두 가지 방식으로 Modal collapse를 해결하였다. GAN은 injective 가정에서 diversity loss를 통해 coverage를 높이는 방식으로 현상을 완화하였지만, 데이터 포인트의 직접 관찰을 통한 복원 시도는 없기에 완전한 해결로 보기는 어렵다.

이런 케이스는 Energy-based GAN 모델이나, Diffusion + GAN 모델을 조금 더 살펴보면 Modal collapse 해결을 위한 좋은 직관을 얻을 수 있지 않을까 싶다.

Additional intuition

그럼 KL-divergence의 entropy term은 Contrastive objective, diversity loss과 본질적으로 다른가

현재는 negative term이 분포 정의에서 자유로운 pratical한 entropy term으로 작용하는 것 아닐까 하는 직관이 있다. 결국 Entropy term, contrastive objective, diversity loss가 본질적으로 같은 것 아닐까 하는 것이다.

그렇다면 우리는 좀 더 통합된 하나의 프레임워크를 구성해 볼 수도 있다.

기본적으로 VAE, Flow 계열 모델은 prior distribution의 가정이 필요하다. GAN은 implicit model로 가정을 우회하고, 보다 sharp한 샘플을 지원한다. implicit model을 상정하고, practical한 entropy를 통해 regularizing할 수 있다면, sharpness와 coverage를 모두 챙길 수도 있을 것이다.

반대로 데이터가 적은 상황이라면, prior에 대한 강한 가정과 analytic한 entropy를 통해 generalization을 일굴 수도 있다.

SurVAE Flows[arXiv:2007.02731]에서는 이런 상황에서 한가지 논의를 더 이어나간다. “그렇다면 반반도 되는가”. implicit model에서 analytic entropy를 구한다거나, explicit model에서 pratical entropy를 구할 수 있는가, 이 때 얻을 수 있는 장점이 있는가의 질문을 던져본다.

Reference

• Tackling the Generative Learning Trilemma with Denoising Diffusion GANs, Xiao et al., 2021. [arXiv:2112.07804]
• NVAE: A Deep Hierarchical Variational Autoencoder, Vahdat and Kautz, 2020. [arXiv:2007.03898]
• Denoising Diffusion Probabilistic Models, Ho et al., 2020. [arXiv:2006.11239]
• Glow: Generative Flow with Invertible 1x1 Convolutions, Kingma and Dhariwal, 2018. [arXiv:1807.03039]
• A Style-Based Generator Architecture for Generative Adversarial Networks, Karras et al., 2018. [arXiv:1812.04948]
• Auto-Encoding Variational Bayes, Kingma and Welling, 2013. [arXiv:1312.6114]
• A Simple Framework for Contrastive Learning of Visual Representations , Chen et al., 2020. [arXiv:2002.05709]
• Wav2Vec2.0: A Framework for Self-Supervised Learning of Speech Representations, Baevski et al., 2020. [arXiv:2006.11477]
• Representation Learning with Contrastive Predictive Coding, Oord et al., 2018. [arXiv:1807.03748]
• StarGAN v2: Diverse Image Synthesis for Multiple Domains, Choi et al., 2019. [arXiv:1912.01865]
• SurVAE Flows: Surjections to Bridge the Gap between VAEs and Flows, Nielsen et al., 2020. [arXiv:2007.02731]