• Marta Garnelo et al., 2018, arXiv
• Keyword: Bayesian, Process
• Problem: Weakness of knowledge sharing and data inefficiency of classical supervised learning
• Solution: Stochastic Process + NN
• Benefits: Data efficient, prior sharing
• Contribution: Encapsulation of parameterized NN function family.
• Weakness or Future work: Global uncertainty, pairwise correlation.

Function Approximation

우리는 데이터의 경향성을 파악해 추론을 얻어내기 위해 흔히 데이터셋 $\lbrace(x_i, y_i)\rbrace^{n-1}_{i=0}$과 함수 $f: X \to Y$를 가정한다. 일반적인 지도학습에서는 $f$를 parameterized model로 가정하고, computation을 고정, parameter를 학습하는 방식을 취한다. 그 이후에는 deterministic하게 입력에 대해 출력이 결정된다. 이러한 방식은 prior의 적용이 한정적이고, 그에 따라 learning 사이의 정보 공유가 어려워 매번 대량의 데이터셋에 대한 새로운 학습이 요구되는 등 여러 한계를 보이기도 한다.

Stochastic process는 함수라는 카테고리를 하나의 확률 분포로 가정한다. 함수에 대한 사전 지식은 분포상의 가정으로 표현되고, 학습은 관측된 값들에 대한 조건부 확률과 사후 분포로써 표현된다.

대표적인 예로 gaussian process는 함수의 smoothness prior를 kernel function으로 나타내었고, 이는 값들 사이의 유사도로 나타나게 된다. 하지만 이러한 메소드들은 prior에 따라서 computationally intractable하기도 하고, $O(N^3)$에 달하는 연산량에 현대에는 많이 쓰이지 않고 있다.

이러한 문제를 풀기 위해 model family를 제안하고, 이것이 Conditional Neural Process 이다.

Stochastic Process

먼저 observation $O = \lbrace(x_i, y_i)\rbrace \subset X \times Y$ 과 target $T=\lbrace x_i\rbrace^{n+m-1}_{i=n}$ 를 가정하자. 이 때 $f: X \to Y$로의 함수와 이 함수의 분포 P가 존재한다면 $f \sim P$ 이고, 조건부 분포 $P(f(T)|O, T)$로 표현된다.

GP에서는 P를 Gaussian으로 가정하고, Covariance Matrix 대신 두 지점 사이의 유사도를 측정하는 kernel 함수를 도입한다. 이러한 모델은 data efficient 하지만, prior나 kernel 함수의 설정이 어렵고, 추론 과정이 $O((n+m)^3)$로 computationally expensive 하다.

Conditional Neural Process (CNPs)

CNP는 함수를 observation에 대한 조건부 분포로 가정한다. CNP는 observation을 고정된 크기의 embedding vector로 표현하고, 이를 토대로 새로운 query에 대한 추론을 만든다. 이 모든 것이 NN을 통한 single forward pass에 이뤄지기 때문에 관측수 n과 쿼리수 m에 대해 O(n + m)의 복잡도만을 요구로 한다.

observation O가 주어질 때 CNP는 $Q_\theta$ 의 conditional process를 가정한다. 기존의 stochastic process처럼 O와 T의 순서에 대해 추론이 변하지 않는 permutation invariance를 보장한다. 또한 factorization $Q_\theta(f(T)|O, T)=\Pi_{x \in T}Q_\theta(f(x)|O, x)$을 가정한다.

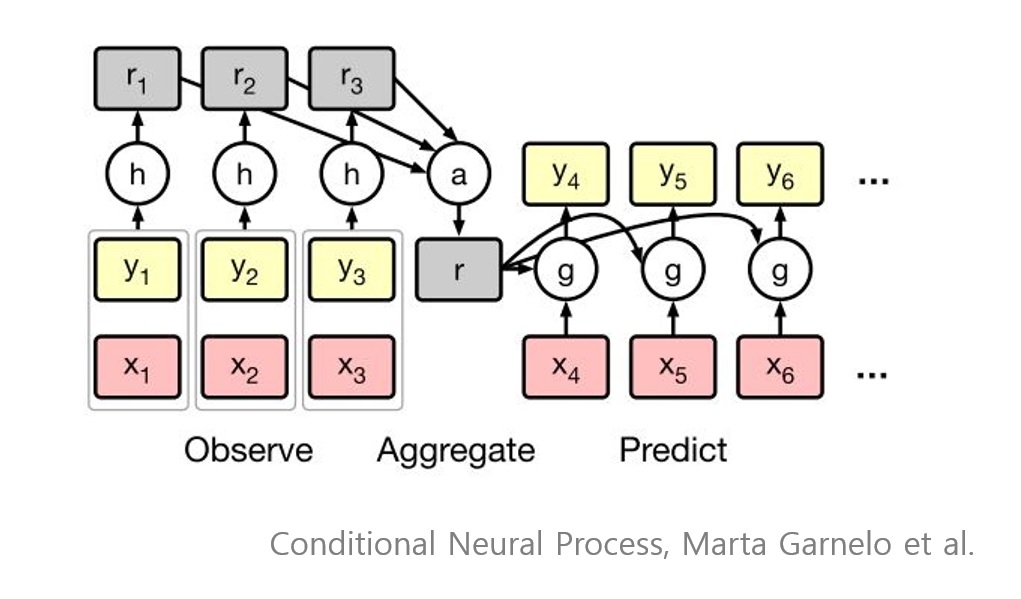
CNP의 구조는 다음과 같다.

$r_i = h_\theta(x_i, y_i) \quad \forall (x_i, y_i) \in O$

$r = \oplus^n_i r_i$

$\phi_i = g_\theta(x_i, r) \quad \forall x_i \in T$

이 때 $h_\theta: X \times Y \to \mathbb R^d$ 이고, $g_\theta: X \times \mathbb R^d \to \mathbb R^e$ 이다. $\oplus$는 observation embedding을 합치는 operation으로 본문에서는 permutation invariance를 지키기 위해 commutative 하다는 가정을 두었다.

그 결과 process는 $Q_\theta(f(x_i) | O, x_i) = Q(f(x_i) | \phi_i)$ 로 표현되며, 이 과정이 NN forward pass만으로 이뤄지기 때문에 O(n + m)의 복잡도를 가진다.

regression 에서는 $\phi_i = (\mu_i, \sigma_i^2)$ 와 $\mathcal N(\mu_i, \sigma_i^2)$ 로 두어 최종 $f(x_i)$가 가우시안을 따르게 하고, classification에서는 categorical distribution의 logits로 두었다.

학습은 nll을 minimize 하는 방식으로 이뤄진다.

$\mathcal L(\theta) = -\mathbb E_{f \sim P}\left[\mathbb E_N\left[\log Q_\theta(\lbrace y_i\rbrace^{n-1}_{i=1}|O_N, \lbrace x_i\rbrace^{n-1} _{i=0})\right]\right]$

Discussion

본문에서는 CNP가 training 데이터에서 prior을 적절히 학습하였고, 이를 통해 observation 간의 learning share이 가능하다고 이야기한다. 실험에서도 보였듯 data efficient하면서도 NN의 adaptivity를 충분히 잘 활용 하였고, meta-learning이나 few-shot learning 과의 상관성에 대해서도 이야기하였다. 지금은 POC 수준이지만, statistical context에서 function family를 적절히 encapsulate 한 것이 주요 contribution이지 않을까 싶다.

추후 Neural Process나 Attentive Neural Process에서도 이야기하지만, CNP는 global uncertainty를 측정하는 수단이나, observation과 target 사이의 correlation을 측정하는 수단이 명시적으로 존재하지 않는다는 점도 고려해야 한다.

Implementation

• Tensorflow v1: tf-neural-process

Reference

• Conditional Neural Processes, Garnelo et al., 2018.