Consistency Models
- Consistency Models, Song et al., 2023. [arXiv:2303.01469]
- Keyword: Consistency Models, Probability Flow ODE
- Problem: Slow generation of Diffuison Models.
- Solution: Map the sample points on a trajectory to a single datum point.
- Benefits: Few-step generation (1 or 2 steps), accelerate the generation speed.
- Contribution: Introduce a new generative model, called Consistency Models.
Introduction
Diffusion Model은 높은 합성 품질을 보이지만, 50~1,000번의 forward pass를 요구하는 등 합성 속도에 한계를 가진다. Diffusion Model은 데이터의 분포에서 사전 분포까지의 forward process를 다회 진행하여, 한 번의 process에서 취급하는 transform의 변량을 작게 유지한다. 이를 통해 inverse process에 필요한 score을 unimodal gaussian으로 근사할 수 있게 되었다.
반대로 forward process의 수가 극도로 줄어, 한 번의 process에서 취급하는 transform의 변량이 커지면, inverse process를 unimodal gaussian으로 근사하는데 한계가 생긴다. 실제로 Diffusion model을 2-steps, 5-steps로 모델링할 경우 학습의 안전성과 샘플의 품질이 떨어진다.
이를 Mitigate 하기 위한 여러 시도가 있었다. Denoising Diffusion GANs[Xiao et al., arXiv:2112.07804]에서는 Score을 implicit model(e.g. GAN)을 통해 모델링하여 분포 형태와 무관히 학습을 수행하고자 하였고, Progressive Distillation[Salimans & Ho, arXiv:2202.00512]에서는 더 많은 스텝에서 학습된 Diffusion Model로부터 Distillation을 수행하기도 한다.
NCSN[Song & Ermon, arXiv:1907.05600]의 저자인 Yang Song은 이에 새로운 모델군인 Consistency Model을 제안한다.
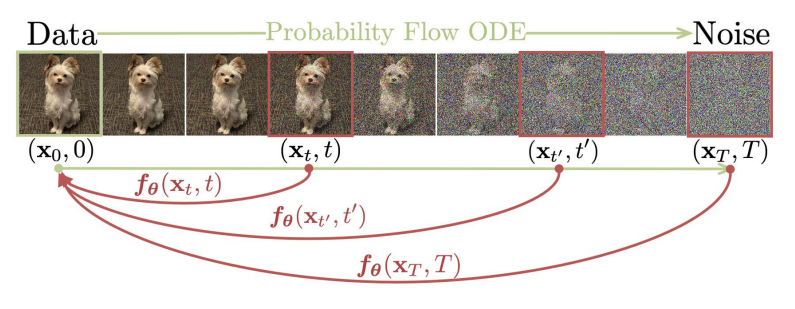
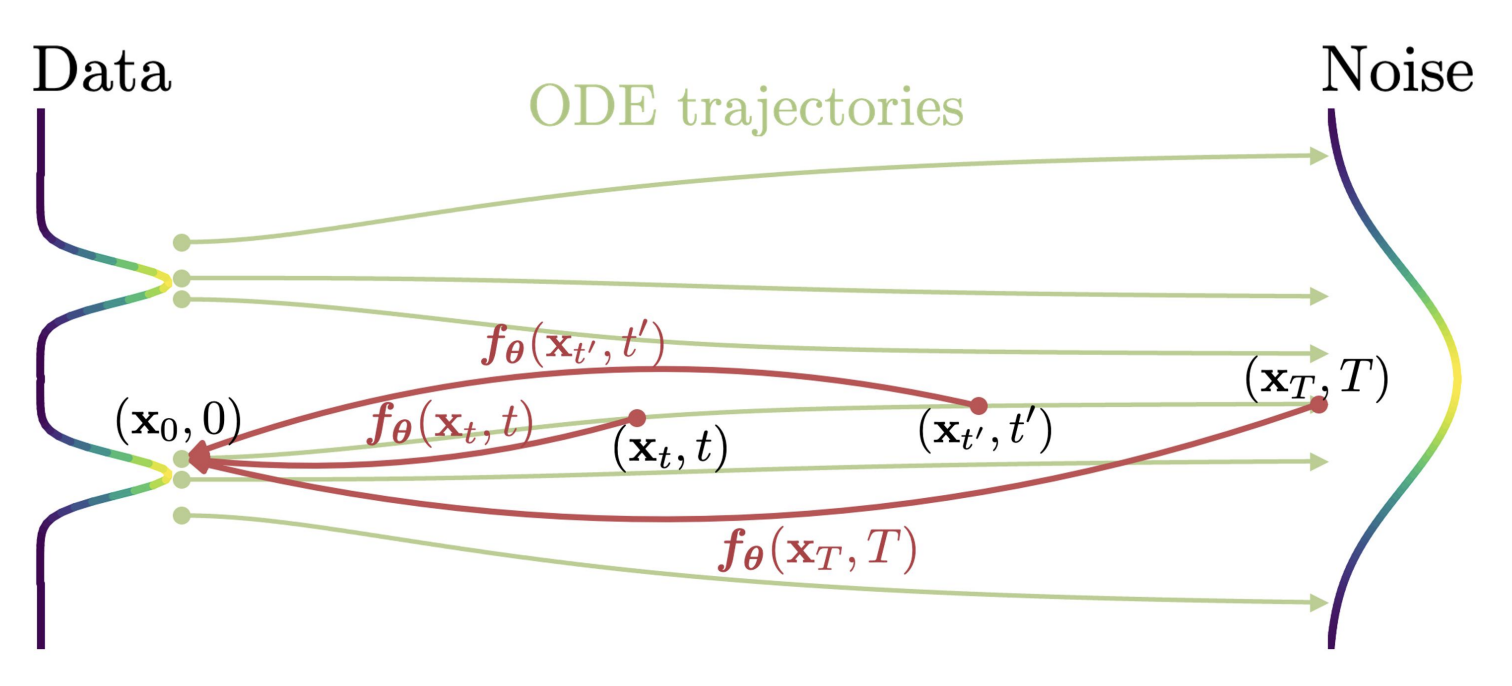
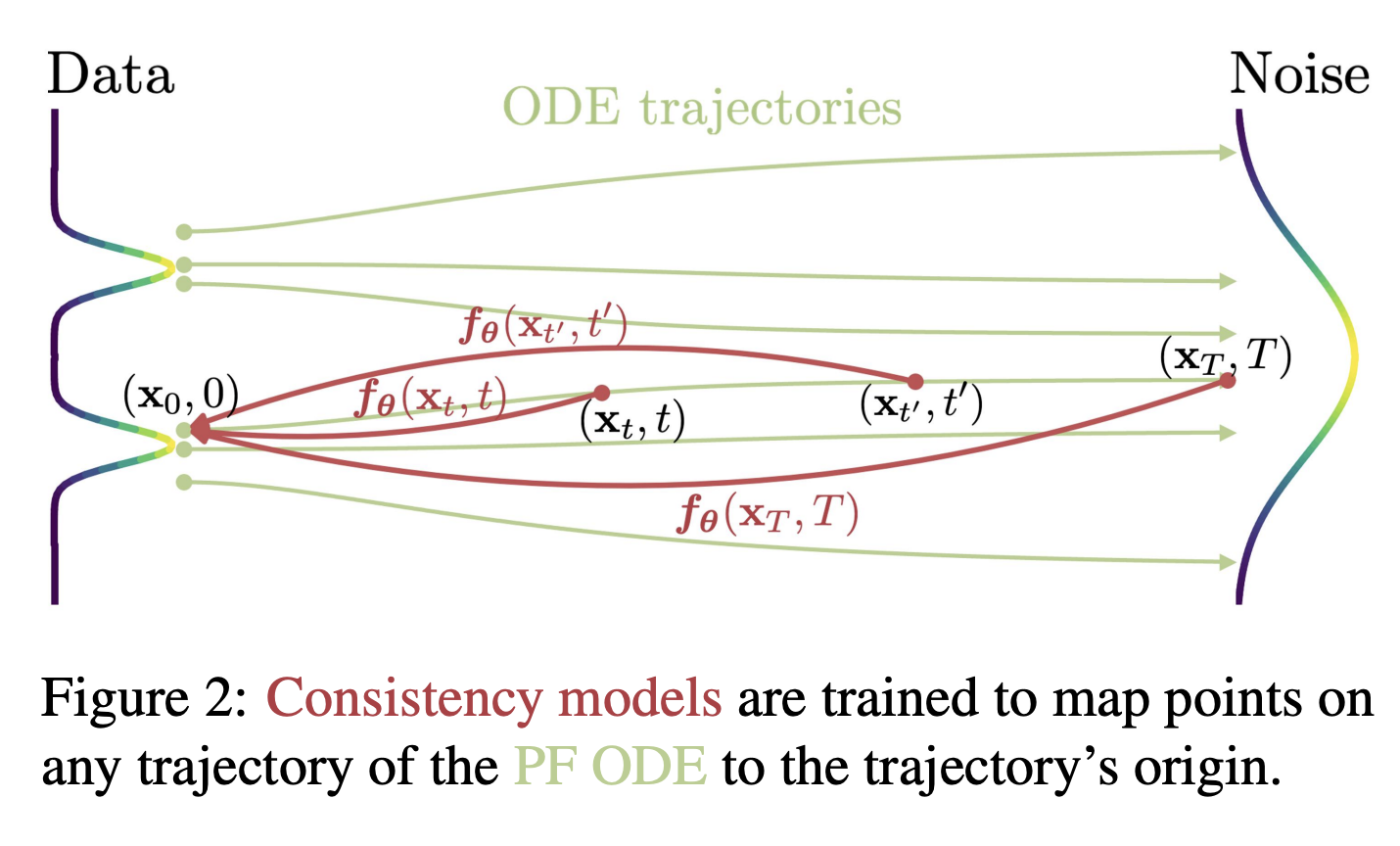
Figure2: We learn to map any point on the ODE trajectory to its origin. (Song et al., 2023)
Score 모델은 사전 분포의 샘플을 데이터 분포로 변환하는 과정에서 궤적(이하 trajectory)을 남긴다. 이때 Langevin-like sampler는 generation 과정에도 소량의 noise를 더해가기에, trajectory의 중간에서 어떤 데이터가 생성될지 추정할 수 없다. 일정 수준 이상의 SNR이 확보된 후에야 샘플의 형태를 어렴풋이 확인하는 정도이다.
DDIM[Song et al., arXiv:2010.02502] 혹은 Probability Flow ODE[Song et al., arXiv:2011.13456]를 가정하여 deterministic trajectory를 구성하더라도, 5~10회 이상의 샘플링을 요구한다.
만약 deterministic trajectory 위의 점이 주어졌을 때 trajectory의 시점을 추정할 수 있다면, 궤적을 따라 샘플링을 수행할 필요 없이 1-step으로 이미지를 생성할 수 있게 된다.
Consistency Model(이하 CM)의 목적은 trajectory 위의 모든 점을 trajectory의 시점으로 매핑시키는 것이다. Trajectory의 종점에 존재하는 tractable noise distribution에서 시작하여 few-step 내에 data distribution sample을 획득하는 것이 목표이다.
Diffusion Models
CM은 continuous diffusion에서 영감을 받았다.
$$\mathrm{d}x_t = \mu(x_t, t)\mathrm{d}t + \sigma(t)\mathrm{d}w_t\ \mathrm{where}\ t\in [0, T],\ T > 0$$
standard brownian motion $w_t$, drift $\mu(x, t) = 0$, diffusion $\sigma(t) = \sqrt{2t}$을 가정하여, $p_t(x) = p_\mathrm{data}(x) \otimes \mathcal N(0, t^2I)$의 variance exploding diffusion을 상정한다. (i.e. tractable prior $\mathcal N(0, T^2I)$)
위 SDE는 Reverse process에 대한 ODE의 존재성을 보장한다. 이를 [Song et al., arXiv:2011.13456]에서는 Probability Flow ODE라 표현한다.
$$\mathrm{d}x_t = \left[\mu(x_t, t) - \frac{1}{2}\sigma(t)^2\nabla\log p_t(x_t)\right]$$
Probability Flow ODE에 앞서 가정한 drift, diffusion term을 대입하면 $\mathrm{d}x_t /\mathrm{d}t = -ts_\phi(x_t, t)$로 정리할 수 있다(이하 Emperical PF ODE). 이에 $\hat x_T \sim \pi = \mathcal N(0, T^2I)$로 ODE를 초기화하면, numerical ode solver를 통해 데이텀 포인트를 획득할 수 있게 된다.
Numerical stability를 위해 $t = \epsilon$에서 정지한다. ($\because \hat x_0 \sim \mathcal N(0, 0)$)
(image를 [-1, 1]의 pixel value로 rescale, T=80, $\epsilon$=0.002로 가정)
Consistency Models
CM은 가장 먼저 $\{x_t\}_ {t\in [\epsilon, T]}$의 Solution trajectory에 대해 Consistency function $f: (x_t, t)\mapsto x_\epsilon$을 정의한다. 이는 trajectory의 두 시점 $t, t’\in[\epsilon, T]$에 대해 $f(x_t, t) = f(x_{t’}, t’)$의 consistency를 보장하고, 종점(사전 분포)을 포함한 trajectory 위 어디서든 데이텀 포인트를 획득할 수 있게 지원한다.
Generation trajectory (Figure 2, Song et al., 2023)
데이터 분포의 시점을 보장하기 위해 $f(x_\epsilon, \epsilon) = x_\epsilon$의 identity function을 가정한다(boundary condition). Free-form Network $F_\theta(x, t)$위에서 boundary condition을 만족하는 함수 $f_\theta(x, t)$는 다음과 같이 표현할 수 있다.
$$f_\theta(x, t) = \left\{\begin{matrix}x & t=\epsilon \\ F_\theta(x, t) & t\in(\epsilon, T]\end{matrix}\right.$$
혹은 다음과 같이도 표현할 수 있다.
$$f_\theta(x, t) = c_\mathrm{skip}(t)x + c_\mathrm{out}(t)F_\theta(x, t)$$
이때 $c_\mathrm{skip}(t)$와 $c_\mathrm{out}(t)$는 $c_\mathrm{skip}(\epsilon) = 1,\ c_\mathrm{out}(\epsilon) = 0$을 만족하는 미분 가능한 함수이다. 디퓨전 모델에서는 후자와 같은 Formulation을 많이 활용해 왔기에, CM은 후자를 가정한다.
이후 사전 분포 샘플 $\hat x_T \sim \mathcal N(0, T^2I)$에 대해 $\hat x_\epsilon = f_\theta(\hat x_T, T)$로 데이텀 샘플을 획득할 수 있게 된다(single-step). 만약 multistep으로 운용할 경우 $\hat x_{\tau_n} \leftarrow x + \sqrt{\tau^2_n - \epsilon^2}z,\ x \leftarrow f_\theta(\hat x_{\tau_n}, \tau_n)$로 $\{\tau_1, …, \tau_{N - 1}\}$에 대해 N회 샘플링을 수행한다.
Training
가장 먼저 제안할 학습 방법은 Score model로부터 Distillation을 받아오는 것이다.
$$t_i = (\epsilon^{1/\rho} + \frac{i-1}{N-1}(T^{1/\rho} - \epsilon^{1/\rho}))^\rho,\ \mathrm{where}\ \rho=7$$
Pretrained score model $s_\phi(x, t)$이 있을 때, range $[\epsilon, T]$를 $N - 1$개 지점으로 양자화한다(discretizing horizon, distillation 과정 중 N의 수를 scheduling 하기 위해).
ODE solver의 update function을 First-order Euler method로 가정 시 (i.e. $\Phi(x, t; \phi) = -ts_\phi(x, t)$), Emperical PF ODE의 Trajectory 위 인접 샘플 포인트는 다음과 같다.
$$\hat x^\phi_{t_n} = x_{t_{n+1}} - (t_n - t_{n+1})t_{n+1}s_\phi(x_{t_{n+1}}, t_{n+1})$$
$x \sim p_{data}, x_{t_{n+1}}\sim\mathcal N(x, t^2_{n+1}I)$의 샘플링 후, adjacent data point pairs $(\hat x^\phi_{t_n}, x_{t_{n+1}})$에 대한 Consistency Distillation(이하 CD) objective는 다음과 같다.
$$\mathcal L^N_{CD}(\theta, \theta^-; \phi) := \mathbb E_{x\sim p_{data}, n\sim \mathcal U(1, N-1)}[\lambda d(f_\theta(x_{t_{n+1}}, t_{n+1}), f_{\theta^-}(\hat x^\phi_{t_n}, t_n))]$$
이때 $\lambda\in\mathbb R^+$, $\theta^-$는 $\theta$의 running average, $d(\cdot, \cdot)$은 metric function이다.
Metric으로는 L2, L1, LPIPS를 후보로, $\lambda = 1$, $\theta^-$는 EMA로 가정한다.
i.e. $\theta^- \leftarrow \mathrm{stopgrad}(\mu\theta^- + (1 - \mu)\theta)$
Analysis를 통해 $f_\theta$가 lipschitz constant를 가질 때 다음을 만족함을 확인할 수 있다. $$\mathcal L^N_{CD}(\theta, \theta; \phi) = 0 \rightarrow \sup_{n, x}||f_\theta(x, t_n) - f(x, t_n; \phi)||^2 = O((\Delta t)^p)\ \mathrm{with}\ p \ge 1$$
$\theta^-$가 EMA이므로, 수렴 상황에서 $\theta = \theta^-$를 가정할 수 있고, T가 충분히 클 때 CM의 성능이 arbitarily accurate 해질 수 있음을 방증한다. 또한 $f_\theta(x, \epsilon) = x$의 identity boundary condition으로 인해 $f_\theta(x, t) = 0$이 되는 trivial solution은 고려하지 않아도 된다.
경우에 따라 극한을 취해 $N\to\infty$ Continuous-time CM을 가정할 수 있지만, jacobian vector product에 대한 미분이 필요하여 현대 딥러닝 프레임워크에서는 연산상 비효율이 존재하고, 관련된 효율적 구현은 appendix에서 논의한다.
Distillation을 하지 않는 Consistency Training(이하 CT)는 unbiased score estimation으로 pretrained score model을 대체한다.
$$\nabla\log p_t(x_t) = -\mathbb E_{x\sim p_{data}, x_t\sim \mathcal (x; t^2I)}\left[\frac{x_t - x}{t^2}|x_t\right]$$
이의 수렴성을 보이기 위해서는, $f_{\theta^-}$가 twice continuously differentiable with bounded second derivatives여야 하고, $\lambda$와 $\mathbb E[||\nabla\log p_{t_n}(x_{t_n})]||^2_2$가 bounded, $\forall t\in[\epsilon, T]: s_\phi(x, t) = \nabla\log p_t(x)$인 경우에 한하여 다음을 만족한다.
$$\mathcal L^N_{CD}(\theta, \theta^-; \phi) = \mathcal L^N_{CT}(\theta, \theta^-) + o(\Delta t)$$ $$\inf_N\mathcal L^N_{CD}(\theta, \theta^-; \phi) > 0 \to \mathcal L^N_{CT}(\theta, \theta^-)\ge O(\Delta t)$$
distillation에 비해 objective가 $o(\Delta t)$만큼 크기에, distillation에 비해 느리게 학습될 것임을 방증한다.
(사견: 이는 score estimator의 variance에 영향을 받을 것으로 추정된다.)
N에 따라 실험을 수행하였을 때, N이 작은 경우 training loss가 조기 수렴하는 경향성을 보였고, N이 클 수록 수렴은 느리지만 샘플 품질이 오르는 것을 확인하였다.
빠른 학습과 샘플 품질의 Trade-off를 위해 N은 학습이 진행됨에 따라 점차 늘리는 방향으로 scheduling하고, 그에 따라 $\mu$는 감소하도록 설계한다.
$$N(k) = \left\lceil\sqrt{\frac{k}{K}((s_1 + 1)^2 - s^2_0) + s_0^2} - 1\right\rceil + 1 \\ \mu(k) = \exp\left(\frac{s_0\log \mu_0}{N(k)}\right)$$
Continuous-time이 되면 schedule function이 필요하지 않지만, 여전히 jacobian vector product에 대한 효율적인 구현이 필요하다.
Experiments
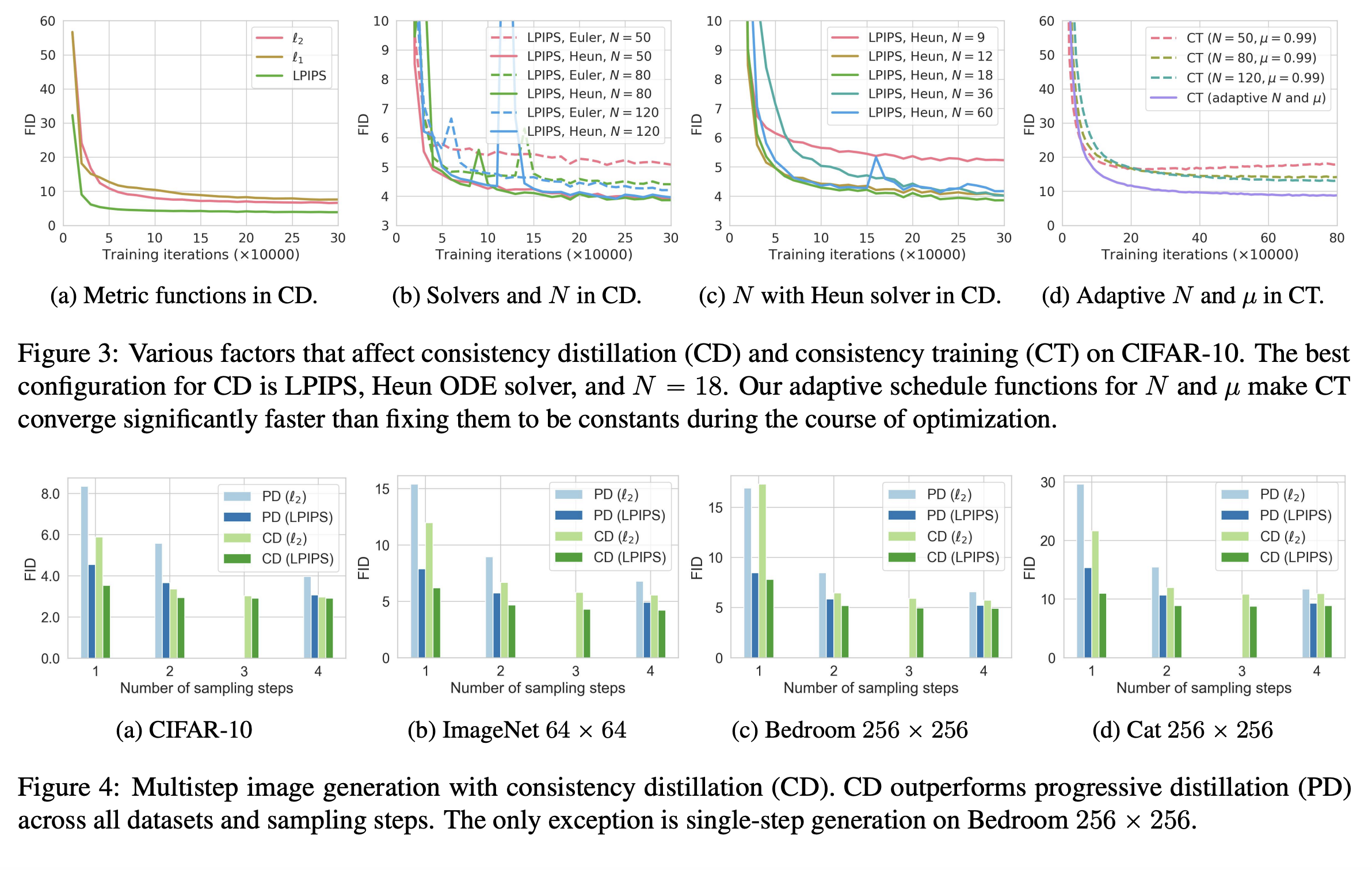
Figure3: Various factors that affect CD and CT / Figure4: Multistep generation. (Song et al., 2023)
Metric function의 경우 LPIPS에서 가장 좋은 성능을 보였다. LPIPS는 Progressive Distillation에서도 유의미한 개선을 보이기도 했다. Consistency Distillation은 Progressive Distillation에 비해 uniform 하게 좋은 성능을 보였고, 샘플링 스텝이 늘어남에 따라 실제로 성능 향상을 보인다.
아쉬운 점은 데이터셋의 이미지가 대개 작다(e.g. cifar-10 32x32, imagenet 64x64, lsun 256x256). FFHQ와 같이 mega pixel image에 대해서도 점검이 되었다면 좋지 않았을까 싶다.
Thoughts
- 왜 PD 보다 CD의 성능이 나은가
PD는 여전히 Score modeling을 가정하기에, distillation을 수행하여도 posterior를 unimodal gaussian으로 근사하는데 한계를 가질 것이다(step 수가 줄어들수록 forward process의 transform 변량이 커지고, 이에 inverse process가 더 복잡한 분포의 형태를 보이므로).
반면 Consistency model은 Score을 모델링하는 것이 아니다. Score model의 trajectory 위에서 주어진 샘플의 시점을 추정한다. 그렇기에 unimodal distribution을 가정할 필요도 없고, 분포 간 괴리를 고려할 이유도 없다. 이러한 점에서 PD에 비해 relaxed condition에서 더 좋은 성능을 보일 수 있던 것 아닌가 싶다.
- 왜 Multistep generation에서 성능이 더 좋은가
잘 학습된 CM 입장에서는 trajectory의 종점에서 샘플 포인트를 추정하는 것 보다, 상대적으로 SNR이 높은 중간 지점에서 샘플 포인트를 추정하기 더 쉬울 것이다(e.g. 원본과의 PSNR이 더 높은 등).
그렇기에 trajectory 위에서 최초 샘플링을 거쳐 이미지의 개형(e.g. low-frequency signal)을 만들고 나면, 이후 noising(on the same trajectory) 후 다시 샘플링을 수행함으로써 더 쉽게 추정된 높은 품질의 이미지를 획득할 수 있던 것 아닐까 싶다.
Wrap up
고민해 보아야 할 부분이 더 있다.
Q. adjacent points를 넘어 더 먼 지점의 샘플을 토대로 학습하면 어떻게 되는가
Q. diffusion model과의 variance 차이는 어떨 것인가 (i.e. langevin-like sampler는 trajectory에 perturbation을 가하는데, DDIM, PF ODE, CM과 같은 모델은 deterministic trajectory를 가정)
Q. Trajectory가 datum point에 대해 유일할 필요는 없는가 (i.e. 현재는 데이터와 사전 분포에서 독립적으로 표본을 획득하고, 이를 토대로 trajectory를 구축하는데, 두 분포를 독립적이라 가정해도 무방한가. 이 trajectory는 generation time에 발생 가능한 true trajectory인가)
관련하여서는 더 고민한 후에 글로 정리할 예정이다.
References
- Consistency Models, Song et al., 2023. [arXiv:2303.01469]
- Progressive Distillation for Fast Sampling of Diffusion Models, Salimans & Ho, 2022. [arXiv:2202.00512]
- Denoising Diffusion GANs: Tackling the Generative Learning Trilemma with Denoising Diffusion GANs, Xiao et al., 2021. [arXiv:2112.07804]
- Score-Based Generative Modeling through Stochastic Differential Equations, Song et al., 2020. [arXiv:2011.13456]
- DDIM: Denoising Diffusion Implicit Models, Song et al., 2020. [arXiv:2010.02502]
- DDPM: Denoising Diffusion Probabilistic Models, Ho et al., 2020. [arXiv:2006.11239]
- NCSN: Generative Modeling by Estimating Gradients of the Data Distribution, Song & Ermon, 2019. [arXiv:1907.05600]