• Hyunjik kim et al., 2019, arXiv
• Keyword: Bayesian, Process
• Problem: Underfitting of Neural Process
• Solution: NP + Self-Attention, Cross-Attention
• Benefits: Improvement of prediction accuracy, training speed, model capability.
• Contribution: Solving underfitting on NP
• Weakness or Future work: Decoder + Self-Attention

Neural Process and Gaussian Process

Neural Process는 함수 분포를 모델링하기 위한 효과적인 메소드를 소개했다. linear time에 작동하며, 한번 학습되면 임의의 context pair와 query에 대해 target 분포를 예측할 수 있다. 그럼에도 NP와 GP를 직접 비교하기 어려운 이유는 NP는 stochastic process의 여러 realization (process에서 샘플링한 함수 표본) 에 대해서 학습하지만, GP는 하나의 realization에서 sample 된 observation에 대해 학습하기 때문이다.

NP는 Scalability, Flexibility, Permutation Invariance라는 점에서 여러 장점이 있지만, consistency 문제를 가지고 있다. 이는 context로부터 target을 추론한 후, 다시 context에 덧붙여 target을 추가 추론했을 때와 온전한 context로부터 전체 target을 추론했을 때 분포차가 발생할 수 있음을 의미한다. 그러므로 NP를 그 자체로 consistent 하다고 보기보다는 consistent stochastic process의 근사라고 보는 것이 맞다.

NP의 또 하나의 약점은 context set에 underfit한다는 것이다. 실제로 1D Curve Fitting 문제를 살펴보면, context point가 존재하는 지점에서도 과한 분산과 부적절한 평균점을 보인다. 본문에서는 이 이유를 NP가 context set을 고정된 크기의 latent로 변환시키는 과정에 permutation invariant function으로 mean-aggregation을 썼는데, 이 과정이 bottleneck으로 작용했기 때문이라고 판단하였다. 이는 모든 컨텍스트에 동일한 가중치를 주었기에, 디코더가 target을 예측할 때 context point로부터 적절한 관련 정보를 제공받지 못하고 있을 것으로 생각한 것이다.

이러한 점을 해결하기 위해서 GP의 kernel function을 차용하였다. kernel은 입력값의 두 지점에 대해서 유사도를 측정하는 도구로 이용되는데, NP에는 이러한 메커니즘이 존재하지 않는 것이다. 그래서 제안하고자 하는 게 Attentive Neural Process (ANPs)이고, 이는 NP에 differentiable attention을 추가하여 context point에 대한 underfit을 줄인 모델이다.

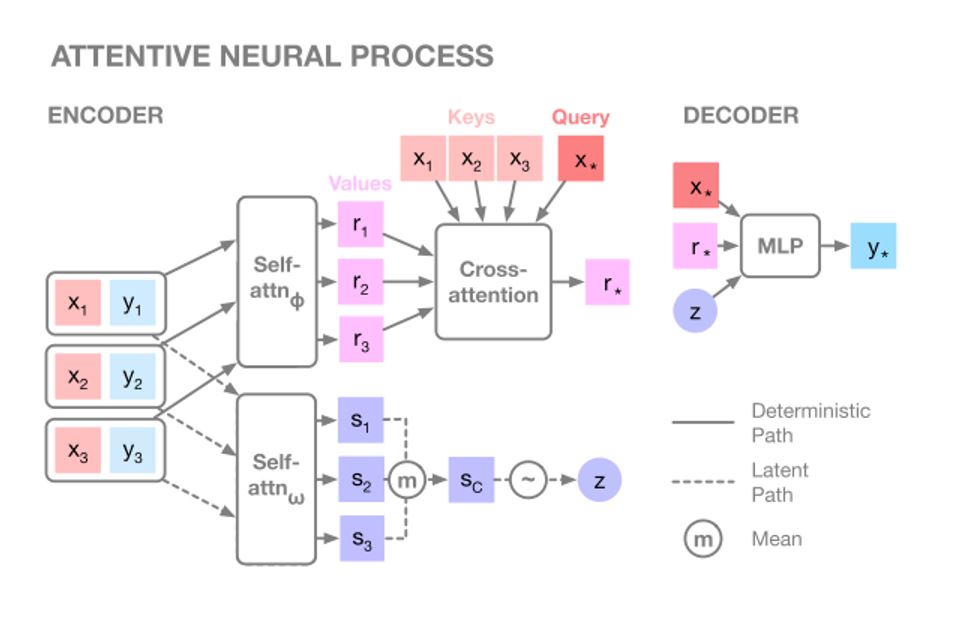
Attentive Neural Process

먼저 입력과 출력 $x_i \in \mathbb R^{d_x}, \ y_i \in \mathbb R^{d_y}$, 그리고 observed context $(x_C, y_C) := (x_i, y_i)_ {i \in C}$ 와 targets $(x_T, y_T) := (x_i, y_i)_{i \in T}$를 가정한다. context representation aggregator r에 대해 $r_C := r(x_C, y_C) \in \mathbb R^d$로 두고, latent encoder s에 대해 $s_C := s(x_C, y_C)$로 두면 NP는 다음을 모델링하는 것과 같다.

$$p(y_T | x_T, x_C, y_C) := \int p(y_T | x_T, r_C, z)q(z | s_C)dz$$

여기서 NP가 가정하는 process F의 randomness는 global latent z에서 오기 때문에 likelihood를 최대화하는 과정은 z의 샘플링을 통해 여러 개로 realization 된 하나의 process를 학습하는 것과 같다.

z_context = self.z_encoder(context, key=cx, query=cx)
z_prob = self.latent_prob(z_context)
latent = z_prob.sample()

self_attend = self.encoder(context, key=cx, query=cx)

ANP는 여기에 두 가지 attention을 덧붙인다. 첫 번째는 self-attention으로 context 사이에서 정보를 공유하고 더 나은 intermediate representation을 만들기 위한 장치이다.

cross_attend = self.cross_encoder(self_attend, key=cx, query=query)
rep = self.decoder(cross_attend, query, latent)
dist, mu, sigma = self.normal_dist(rep)

context에 self-attention을 취하면 context 개수만큼의 intermediate representation(IR)이 생기고, 이는 target과 context의 유사도를 비교하는 cross attention을 통과하여 query-specific representation $r_* := r^*(x_C, y_C, x_ *)$을 만든다. 이는 모델이 실제로 어떤 컨텍스트 포인트를 조명할지 명시하기 때문에 target prediction에 도움을 줄 수 있다.

latent encoder의 경우에는 self-attention 이후 cross-attention 대신에 mean-aggregation을 선택했는데, 본문에서는 이를 global-latent로써 보존하고 싶었다고 한다. latent path에 cross-attention이 들어오면, latent에 locality가 발생하기 때문이다.

$$\log p(y_T | x_T, x_C, y_C) \ge \mathbb E_{q(z | s_T)} \left[ \log p(y_T | x_T, r_C, z) \right] - D_{KL}(q(z | s_T) || q(z | s_C))$$

training loss는 ELBO를 동일이 가져간다.

이렇게 하면 computational complexity가 O(n(n + m))이 되는데, 이는 attention 과정에서 모든 컨텍스트를 탐방하기 때문이다. 하지만 dot-product attention 같은 matrix-multiplication 기반의 attention 알고리즘을 이용하면 대부분이 parallel 하게 동작할 수 있으므로 실제로는 training time이 NP와 비교할 만 하다고 한다.

Discussion

ANP는 attention mechanism을 통해 underfitting problem을 효과적으로 풀어냈다. 추측의 정확도가 높아졌고, 학습이 빨라졌으며, 모델링 할 수 있는 메소드의 범위도 늘었다. 저자는 ANP의 decoder에 self-attention을 붙여 expressiveness의 향상 정도를 확인하고 싶다고 한다. 하지만 이는 target prediction 사이에 상관성이 생기는 문제이니 ordering이나 grouping을 어떻게 해야 할지가 중요해질 것이라고 한다.

Implementation

• Tensorflow v1: tf-neural-process

Reference

• Conditional Neural Processes, Garnelo et al., 2018.
• Neural Processes, Garnelo et al., 2018.
• Attentive Neural Processes, Kim et al., 2019.