ANF, VFlow
- ANF, Augmented Normalizing Flows: Bridging the Gap Between Generative Flows and Latent Variable Models, Huang et al., 2020, arXiv
- VFlow: More Expressive Generative Flows with Variational Data Augmentation, Chen et al., 2020, arXiv
- Keyword: Bayesian, Normalizing Flow, ANF, VFlow
- Problem: Dimensionality problem on normalizing flow
- Solution: Augmentation
- Benefits: Can propagate higher features to flow, better quality, bpd, etc.
- Weakness or Future work: -
Series: Normalizing flow
- Normalizing flow, Real NVP [link]
- Glow, Flow++ [link]
- ANF, VFlow [this]
- i-ResNet, CIF [link]
- SurVAE Flows [link]
Normalizing flow - Bottleneck problem
Normalizing flow는 latent variable model의 한 축으로 자리 잡아 가고 있다. bijective를 통한 change of variables를 근간으로 하기에, 1) network의 inversion이 efficient 해야 하고, 2) log-determinant of jacobian 연산이 tractable 해야 하며, 3) 네트워크가 충분히 expressive 해야 한다.
1)과 2)를 위해서는 기존과 같은 nonlinearity 기반의 레이어를 활용할 수 없었기에, 주로 jacobian의 형태를 제약하는 방식의 부가적인 engineering이 요구되었다.
이 과정에서 mapping의 형태에 제약이 발생했고, 이에 따른 표현력 절감을 완화하기 위해 Glow[3], Flow++[4]과 같이 engineered bijective에 대한 연구가 등장했다.
bijective로의 constraint는 tensor의 dimension도 바꿀 수 없게 하였다. 간단하게 tensor slice를 상정한다면, inverse 과정에서 유실된 slice를 복원해야 하고, 충분히 잘 구성된 상황을 가정하지 않은 이상, 이 과정은 analytic 하게 구성되지 않을 것이다.
$$y = x_{1:d} \ \ \mathrm{where} \ x \in \mathbb R^D, \ d < D \\ x_{1:d} = y, \ \ x_{d+1:D} = \ ?$$
Universal approximation theorem에서부터 WideResNet[5]으로 이어져 오면서 network의 width는 성능에 중요한 factor가 되었다.
이러한 상황에서 tensor의 dimension을 임의로 조작하지 못해 하위 flow에 internal hidden layers의 higher dimensional feature를 충분히 전달하지 못하면, flow는 매번 부족한 정보를 local-dependency부터 다시 추출해야 한다. 이렇게 개개 블럭의 표현력이 떨어진 flow는 block의 수를 늘림으로써 이를 해결해야 했고, computational inefficiency로 이어졌다.
이 때문에 Flow++[4]에서는 global-dependency를 보다 효율적으로 탐색하기 위해 Transformer[6] 기반의 internal network를 제안하기도 한다.
Dimension problem, bottleneck problem의 요점은 high-resolution, low-dimension의 입력에서부터 high-dimension의 feature를 연산하고, 재사용할 수 있는지에 존재한다.
Augmented Normalizing Flow, 이하 ANF[1]와 VFlow[2]는 서로 다른 논문이지만 normalizing flow의 dimension 문제에 대해 augmentation이라는 동일한 해결책을 제시한다.
Augmentation
흔히 Augmentation이라 하면 데이터의 양을 늘리거나, 모델의 robustness를 위한 preprocessing 작업 정도를 상상하겠지만, normalizing flow에서는 input에 추가적인 latent를 concat 하여 입출력 dimension을 직접 늘리는 행위를 이야기한다.
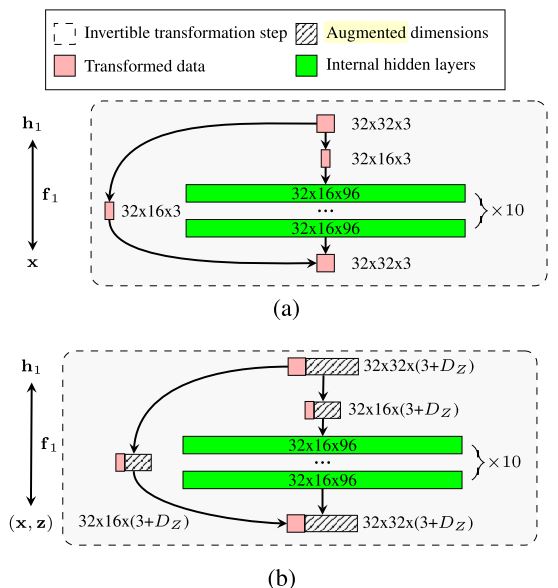
Figure 1: Bottleneck problem in Flow++ and solution VFlow. (Chen et al., 2020)
ANF Perspective
ANF[1]는 dimension을 늘리기 위해 독립 변수 $e \sim q(e) = \mathcal N(0, I)$를 상정하고, family of joint density models $\{ p_\pi(x, e): \ \pi \in \mathfrak B\mathcal{(X \times E)} \}$를 구성한다. 이 과정에서 $p_\pi(x)$의 marginal likelihood 대신에 $p_\pi(x, e)$의 joint likelihood를 다루게 되었다.
$$\hat\pi_\mathcal{A} := {\arg\max}_{\pi \in \mathfrak B(\mathcal{X\times E})}\mathbb E _{(x, e) \sim \hat q(x)q(e)}[\log p _\pi(x, e)]$$
이렇게 확장된 estimator를 ANF[1]에서는 Augmented Maximum Likelihood Estimator (AMLE)라 명명하고, 학습에는 entropy $H(e)$를 활용한 maximizer $\mathcal{L_A}(\pi; x) := \mathbb E_e[\log p_\pi(x, e)] + H(e)$를 정의하여 이용하게 된다. 이렇게 되면 marginal과의 차이는 KL divergence로 유도되고, 원문에서는 이를 augmentation gap이라 칭한다.
$$\begin{align*} &\log p_\pi(x) - \mathcal{L_A}(\pi; x) \\ &= \log p_\pi(x) - \mathbb E_e[\log p_\pi(x) + \log p_\pi(e|x)] - H(e) \\ &= D_\mathrm{KL}(q(e)||p_\pi(e|x)) \end{align*}$$
exact marginal likelihood는 analytic 하게 연산할 수 없으므로, $q(e)$의 K개 i.i.d. sample을 통해 값을 추정해야 한다.
$$\hat{\mathcal L_{A, K}} := \log\frac{1}{J}\sum^K_{j=1}\frac{p_\pi(x, e_j)}{q(e_j)}$$
네트워크는 affine coupling으로 구성하며, Glow[3]에서 split-concat을 활용했던 것과 유사하게 입력 데이터로 구성된 block $x$와 augmentation block $e$를 두고 coupling을 진행한다.
$$\begin{align*} &g_\pi^\mathrm{enc}(x, e) = \mathrm{concat}(x, s_\pi^\mathrm{enc}(x) \odot e + m_\pi^\mathrm{enc}(x)) \\ &g_\pi^\mathrm{dec}(x, e) = \mathrm{concat}(s_\pi^\mathrm{dec}(e)\odot x + m_\pi^\mathrm{dec}(e), e) \end{align*} \\ G_\pi = g_{\pi_N}^\mathrm{dec} \circ g_{\pi_N}^\mathrm{enc} \circ … \circ g_{\pi_1}^\mathrm{dec} \circ g_{\pi_1}^\mathrm{enc}$$
VFlow Perspective
VFlow[2] 또한 마찬가지로 additional random variable $z \in \mathbb R^{D_z}$를 상정하고, data $x \in \mathbb R^{D_X}$와 augmented distribution $p(x, z; \theta)$을 구성한다.
$$e = f(x, z; \theta) \in \mathbb R^{D_X + D_Z}$$
이렇게 되면 marginal이 intractable 하기에, VFlow[2]에서는 variational $q(z|x; \phi)$를 상정하고, lower bound를 objective로 구성한다.
$$\log p(x; \theta) \ge \mathbb E_{q(x|z; \phi)}[\log p(x, z; \theta) - \log q(z|x; \phi)]$$
마찬가지로 density estimation은 sampling을 통해 진행한다.
$$\log p(x; \theta) \simeq \log\left(\frac{1}{S}\sum^S_{i=1}\frac{p(x, z_i; \theta)}{q(z_i|x; \phi)}\right) \ \ \mathrm{where} \ \ z_1, …, z_S \sim q(z|x; \phi)$$
이 때 variational $q(z|x; \phi)$는 보다 유연한 근사를 위해 또 다른 conditional flow로 구성한다.
$$z = g^{-1}(e_q; x, \phi) \Rightarrow \log q(z|x; \phi) = \log p_\epsilon(e_q) - \log\left|\frac{\partial z}{\partial e_q}\right|$$
Between ANF and VFlow
두 접근 모두 augmentation을 통해 bottleneck problem을 풀었다는 것에는 동일하나, formulation이 사뭇 다르게 보인다.
ANF의 경우에는 $q(e)$를 standard normal로 가정하여, entropy of e를 통해 lower bound를 산출해 낸다. 이 경우 augmentated gap $D_\mathrm{KL}(q(e)||p_\pi(e|x))$은 $x$에 독립인 marginal $q(e)$를 모델링하는 과정에서의 incapability에 의해 발생한다.
하지만 VFlow의 경우에는 augmented distribution을 variational $q(z|x)$로 상정하여 intractable marginal의 lower bound에 접근하면서 augmented gap $D_\mathrm{KL}(q_\phi(z|x)||p(z|x))$을 줄일 가능성을 제시한다.
이 두 formulation을 보면 언뜻 ANF는 joint를 VFlow는 marginal을 학습하는 차이가 있어 보이지만, entropy가 더해진 ANF의 maximizer $\mathcal{L_A}(\pi; x)$는 사실 variational distribution을 $q(z|x) = p(z) = \mathcal N(0, I)$의 independent standard gaussian으로 상정한 VFlow의 marginal formulation과 동일하다.
$$\begin{align*} &\log p(x; \theta) \\ &\ge \mathbb E_{z\sim q(z|x)}[\log p(x, z; \theta) - \log q(z|x)]\\ &= \mathbb E_{z \sim p(z)}[\log p(x, z; \theta)] + \mathbb E_{z \sim p(z)}[- \log p(z)] \\ &= \mathbb E_{z \sim p(z)}[\log p(x, z; \theta)] + H(z) \\ &= \mathcal{L_A}(\theta;x) \end{align*}$$
즉 ANF는 trivial distribution을, VFlow는 conditional flow를 기반으로 한 variational distribution을 상정한 것에 차이가 있다.
Connection to Vanilla Generative Flows
이렇게 bottleneck problem을 해결했다지만, 정말로 marginal likelihood의 향상에 도움이 있는지 VFlow[2]에서는 그 증명을 통해 알아본다.
이론상 증명을 알아보기 이전에 notation을 정리한다.
- vanilla generative flow는 $p_x(\mathbf x; \theta_x), \ \theta_x \in \Theta_x$로 정의, $\Theta_x$는 parameter space.
- $D_Z > 0$일 때, VFlow는 $p_a(\mathbf x, \mathbf z; \theta_a), \ z \in \mathbb R^{D_Z}, \ \theta_a \in \Theta_a$, 그리고 marginal $p_a(\mathbf x; \theta_a)$
- $D_Z > 0$일 때, variational $q(z|x; \phi), \ z \in \mathbb R^{D_Z}, \phi \in \Phi$
이때의 maximum liklihood는 vanilla의 경우 $\max_{\theta_x}[\log p_x(\mathbf x; \theta_x)]$, vflow의 경우 $\max_{\theta_a, \phi}\mathbb E_{\hat p(x)q(z|x; \phi)}[\log p_a(\mathbf x, \mathbf z; \theta_a) - \log q(z|x; \phi)]$로 구성될 것이다.
VFlow[2]는 다음과 같은 가정을 한다.
A1. (high-dimensional flow can emulate low-dimensional flow) 모든 $\theta_x \in \Theta_x$와 $D_Z > 0$에 대해 다음을 만족하는 $\theta_a \in \Theta_a$가 존재한다.
$$p_a(\mathbf x, \mathbf z; \theta_a) = p_x(\mathbf x; \theta_x)p_\epsilon(z) \ \forall \mathbf x, \mathbf z$$
A2. (the variational family has an identity transformation) 모든 $D_Z > 0$에 대해 $\phi \in \Phi$가 존재하여, $q(\mathbf z|\mathbf x; \phi) = p_\epsilon(\mathbf z) \ \forall \mathbf x, \mathbf z$를 만족한다.
이는 RealNVP[8], Glow[3] 대부분의 invertible transformation에 성립한다고 한다.
간단한 예로 orthonormal matrix $\theta_x \in \Theta_x$에 대한 invertible linear flow $\epsilon = \mathbf x\theta_x$를 상정한다면, $\theta_a$를 적절히 취함으로써 A1을 만족시킬 수 있다.
$$\theta_a = \left[\begin{matrix}\theta_x & 0 \\ 0 & I\end{matrix}\right] \\ p_a(\mathbf x, \mathbf z; \theta_a) = p_\epsilon\left([\mathbf x, \mathbf z]\left[\begin{matrix}\theta_x & 0 \\ 0 & I\end{matrix}\right]\right) = p_\epsilon(\mathbf x \theta_x)p_\epsilon(\mathbf z)$$
또한 $q(\mathbf z|\mathbf x; I) = p_\epsilon(\mathbf z I) = p_\epsilon(z)$이므로 A2도 만족한다. 추가적인 transform에 대한 증명은 VFlow[2]의 Appendix A.에서 확인 가능하다.
Theorem. A1과 A2의 가정 하에 $D_Z > 0$을 취하면 다음을 얻을 수 있다.
$$\max_{\theta_x \in \Theta_x}\mathbb E_{\hat p(\mathbf x)}\log p_x(\mathbf x; \theta_x)] \le \max_{\theta_a \in \Theta_a, \phi \in \Phi}\mathbb E_{\hat p(\mathbf x)q(\mathbf z|\mathbf x; \phi)}[\log p_a(\mathbf x, \mathbf z; \theta_a) - \log q(\mathbf z|\mathbf x; \phi)]$$
pf. vanilla $p_x(\mathbf x; \theta_x)$에 대해 A1과 A2를 가정하면 다음을 구성할 수 있다.
- $\theta(\theta_x) \in \Theta_a$에 대해 $p_a(\mathbf x, \mathbf z; \theta(\theta_x)) = p_x(\mathbf x; \theta_x)p_\epsilon(\mathbf z)$을 구성. 이는 z를 최소한으로 활용하는 경우를 가정한다.
- $\phi \in \Phi$에 대해 $q(\mathbf z|\mathbf x; \phi) = p_\epsilon(\mathbf z)$. 이는 posterior의 정보를 활용하지 않는 경우를 가정한다.
이의 lower bound는 vanilla와 동일해진다.
$$\log p_a(\mathbf x, \mathbf z; \theta(\theta_x)) - \log q(\mathbf z|\mathbf x; \theta_x) = \log p_x(\mathbf x; \theta_x)$$
이에 대해 다음과 같은 전개가 가능하다.
$$\begin{align*} &\max_{\theta_x \in \Theta_x} \mathbb E_{\hat p(\mathbf x)}[\log p_x(\mathbf x; \theta)] \\ &= \max_{\theta_a \in \Theta_a, \phi \in \Phi} \mathbb E_{\hat p(\mathbf x)p_\epsilon(\mathbf z)}[\log p_x(\mathbf x; \theta) + \log p_\epsilon(\mathbf z) - \log p_\epsilon(\mathbf z)] \\ &= \max_{\theta_x \in \Theta_x} \mathbb E_{\hat p(\mathbf x)}[\log p_a(\mathbf x, \mathbf z; \theta(\theta_x)) - \log p_\epsilon(\mathbf z)] \\ &\le \max_{\theta_a \in \Theta_a} \mathbb E_{\hat p(x)}[\log p_a(\mathbf x, \mathbf z; \theta_a) - \log p_\epsilon(\mathbf z)] \tag 1\\ &= \max_{\theta_a \in \Theta_a} \mathbb E_{\hat p(x)}[\log p_a(\mathbf x, \mathbf z; \theta_a) - \log q(\mathbf z|\mathbf x; \phi)] \\ &\le \max_{\theta_a \in \Theta_a, \phi \in \Phi}\mathbb E_{\hat p(\mathbf x)}[\log p_a(\mathbf x, \mathbf z; \theta_a) - \log q(\mathbf z|\mathbf x; \phi)] \tag 2 \end{align*}$$
1번 식에서는 $\theta_a$의 자율성에 의해, 2번 식에서는 variational $q(z|x;\phi)$의 학습에 의해 부등호가 성립한다. 따라서 이는 ANF와 같이 trivial $q(\mathbf z|\mathbf x) = p_\epsilon(\mathbf z)$를 상정하더라도 기존보다 성능향상이 있음을 의미한다.
VFlow[2]에서는 실험적으로도 channel 수에 따른 bpd 감소를 보였다.
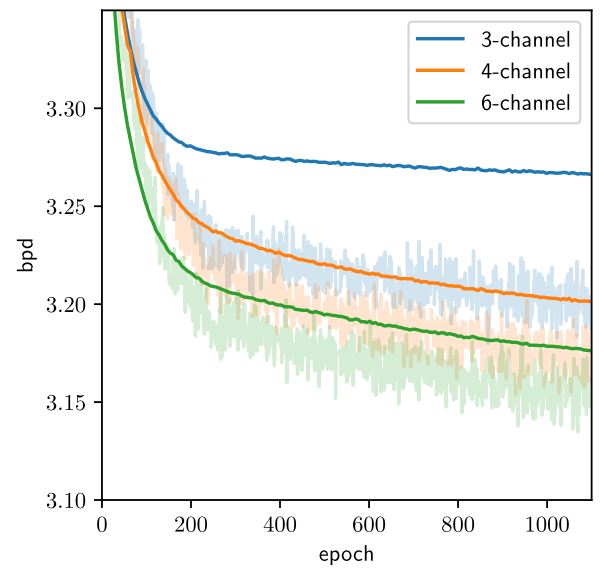
Figure 6. Bpd on training (light) and validation (dark) dataset of Flow++ and VFlow under a 4-million parameter budget (not fully converged) (Chen et al., 2020)
augmentation의 문제를 parameter의 증가라 볼 수도 있는데, VFlow[2]는 hidden layers의 크기를 줄여 parameters 수를 일정 수준 유지하더라도, dimension 자체를 늘리는 것이 더욱 효율적이었음을 보인다.
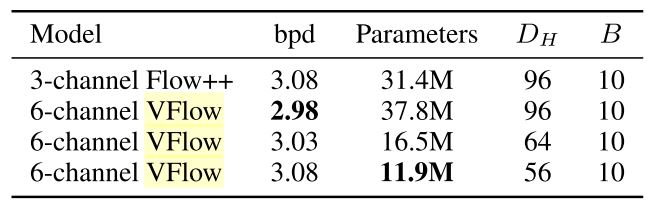
Table 3. Parameter efficiency on CIFAR-10. (Chen et al., 2020)
Connection to VAE
VAE[7]는 1-step augmented flow의 special case로 볼 수도 있다. joint distribution을 gaussian factorizing $p(x, z) = \mathcal N(z; 0, I)\mathcal N(x; \mu(z), \exp(\sigma(z))^2)$을 통해 affine coupling의 1-step flow로 구성하면, vflow의 variational $q(z|x)$에 대해 Gaussian VAE와 동치이다.
$$\epsilon_Z \sim q(z|x) \ \ \epsilon_X \sim \mathcal N(0, I) \\ z = \epsilon_Z, \ \ x = \mu(\epsilon_Z) + \exp(s(\epsilon_Z)) \circ \epsilon_X$$
VFlow[2]는 $p(x, z) = p(z)p(x|z)$라는 hierarchy를 가정하지 않는다는 점에서 보다 일반화된 모델로 볼 수 있다. 또한 이렇게 hierarchy를 구성하면 여전히 $p(x|z)$의 dimension은 고정되고, 정보 공유가 없기에 bottleneck problem은 해결되지 않는다.
VAE[7]는 또한 이러한 hierarchy에 의해 variational $q(z|x)$의 표현력이 중요해지는데, VFlow[2]에서는 이 역할이 $p(x, z)$로 분배되기 때문에 unconditional $q(z|x) = p(z)$를 가정하더라도 ANF[1]와 같이 충분히 좋은 성능을 보일 수 있었다.
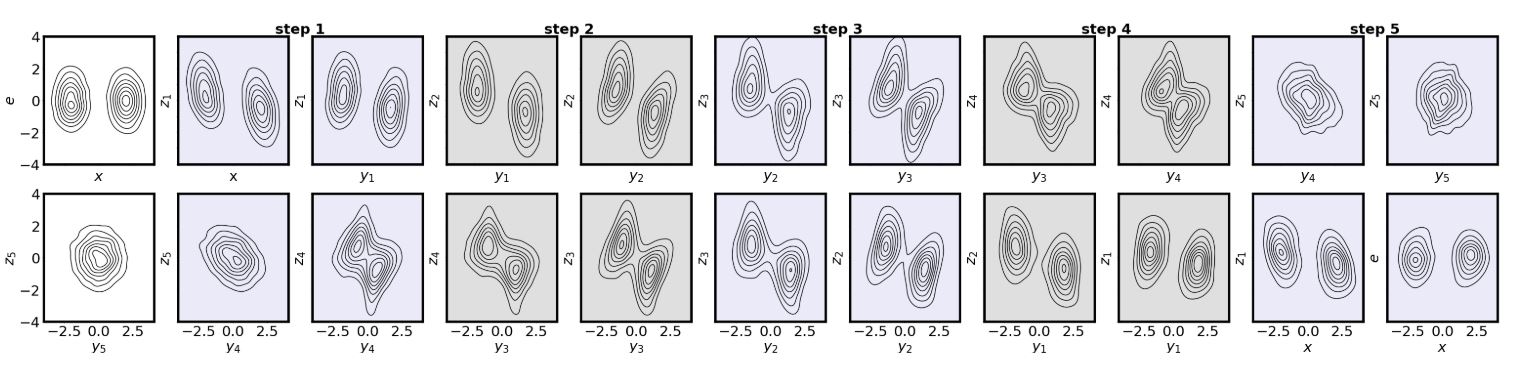
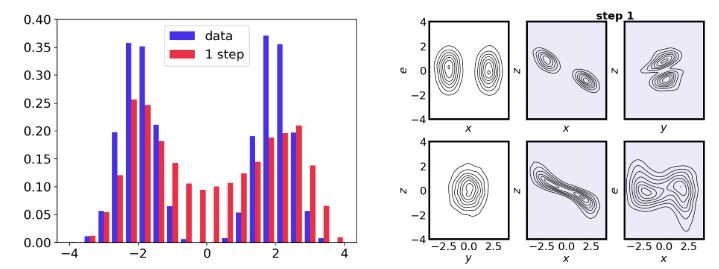
Figure 4: 5-step ANF on 1D MoG. (Huang et al., 2020)
실제로 ANF[1]에서는 실험을 통해 step 수에 따른 latent의 gaussianize 여부를 plotting 해보았는데, step 수가 많아짐에 따라 latent가 gaussian prior에 더욱 근접했음을 확인할 수 있었다.
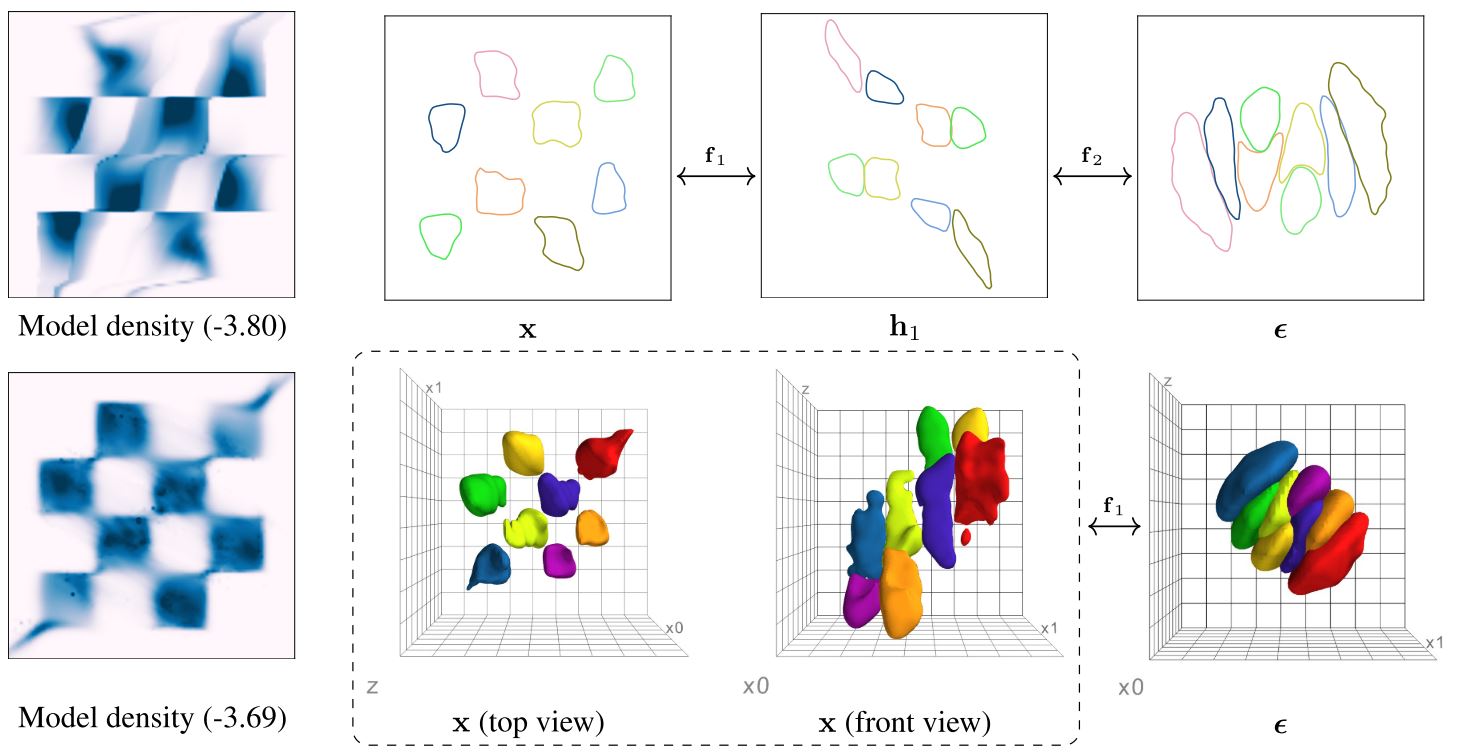
Figure 4: Visualization of learnt transformation on toy data. (Chen et al., 2020)
Modeling Discrete Data
Flow++[4]에서는 discrete data를 위해 variational dequantization을 이야기했었는데, VFlow[2]에서는 augmentation $\mathbf z$와 dequantization $\mathbf u$의 hierarchy를 두어 dicrete modeling을 구성하였다.
$$\log P(\mathbf x) \ge \mathbb E_{r(\mathbf u|\mathbf x),q(\mathbf z|\mathbf x + \mathbf u)}[\log p(\mathbf x + \mathbf u, \mathbf z) - \log r(\mathbf u|\mathbf x) - \log q(\mathbf z | \mathbf x + \mathbf u)]$$
Hierarchical ANF
ANF[1]는 이를 한단계 더 일반화한 Hierarchical ANF를 제안한다. dequantization과 single augmentation이 아닌, augmentation latents $\{z_i\}_{l=1}^L$를 두고 각각의 latent에 hierarchy를 구성하는 방식이다.
$$p(x, z-1, …, z_L) = p(x|z_1, …, z_L)\prod^L_{l=1}p(z_l|z_{l+1}, …, z_L) \\ q(z_1, …, z_L|x) = \prod^L_{l=1}q(z_l|z_1, …, z_{l-1}, x)$$
Experiments
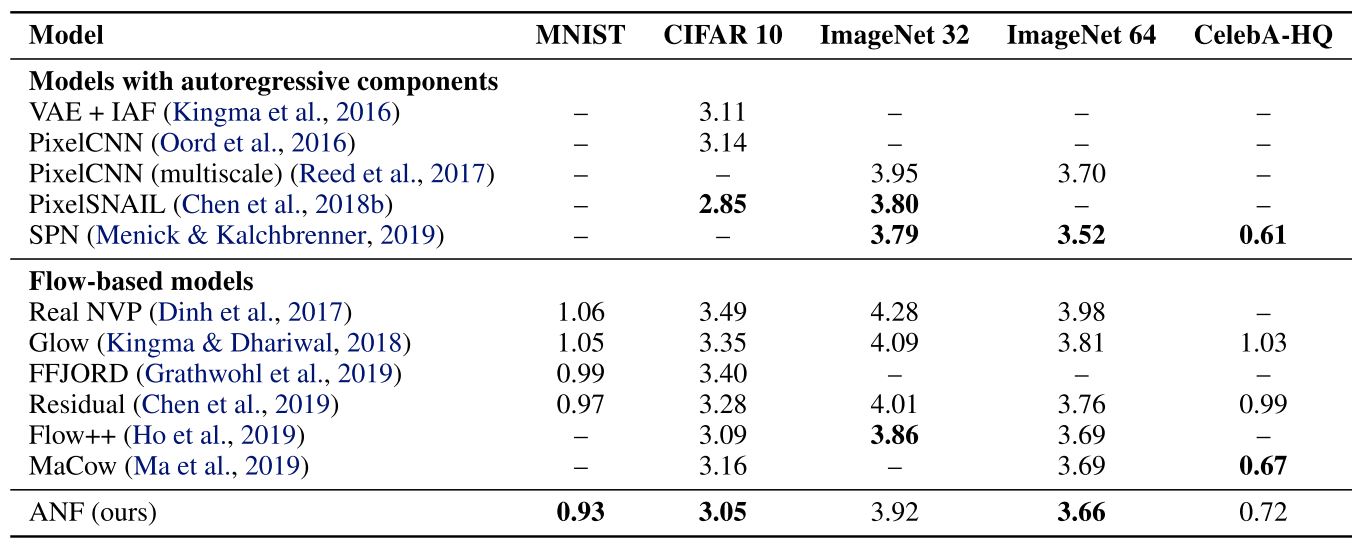
Table 1. Bits-per-dim estimates of standard benchmarks (the lower the better). (Huang et al., 2020)
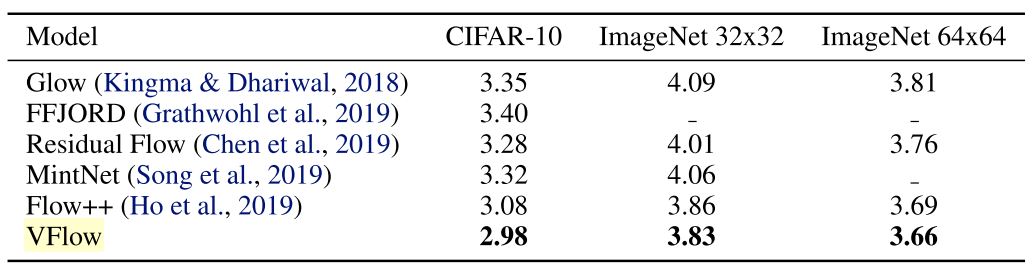
Table 1. Density modeling results in bits/dim (bpd). (Chen et al., 2020)

Table 2. Evaluation on Inception Score (IS, the higher the better) and Fréchet Inception Distance (FID, the lower the better) (Huang et al., 2020)

Figure 8. Left: comparison of linear and rescaled interpolations. Right: rescaled interpolation of input data (first and last columns). (Huang et al., 2020)
ANF[1]는 gaussian prior에서의 linear interpolation은 non-smooth transition을 포함하고 있다고 이야기한다. 이는 gaussian samples가 shell 근처에 중심적으로 분포해 있기 때문이기에, 이에 맞춘 rescaled interpolation이 필요하다는 것이다.
$$h’(u, v, t) = \frac{h(||u||, ||v||, t)}{||h(u, v, t)||}\cdot h(u, v, t)$$
이에 대한 비교는 ANF[1]의 Appendix A.에서 확인 가능하다.
Discusion
사견:
이번에는 augmented flow에 대해 알아보았다. 기존보다 정량적, 정성적 향상이 있었음을 확인했고, VAE와 동치인 case도 보였다. GAN, VAE, Flow라 불리던 stochastic model의 한 축이 통합된 현장이다.
이 외에도 다음에 알아볼 논문에서는 diffusion, rad와 같은 접근까지 unifying 한 framework를 제안하기도 한다. 어쩌면 미래에는 GAN과의 연관성을 통해 major 확률 모델의 통합을 이뤄낼지도 모른다.
representation learning, unsupervised, probabilistic modeling 등 데이터의 표현에 대한 여러가지 연구가 있었지만, 그들을 엮어냈다는 점에서 특히 눈에 띄는 논문인 것 같다.
Reference
[1] Huang, C., Dinh, L. and Courville, A. Augmented Normalizing Flows: Bridging the Gap Between Generative Flows and Latent Variable models. 2020.
[2] Chen, J., et al. VFlow: More Expressive Generative Flows with Variational Data Augmentation. In ICML 2020.
[3] Kingma, D. P. and Dhariwal, P. Glow: Generative Flow with Invertible 1x1 Convolutions. In NIPS 2018.
[4] Ho, J. et al. Flow++: Improving flow-based generative models with variational dequantization and architecture design. In ICML 2019.
[5] Zagoruyko, S. and Komodakis, N. Wide Residual Networks. 2016.
[6] Vaswani, A., et al. Attention is all you need. In NeurIPS 2017.
[7] Kingma, D. P. and Welling, M. Auto-encoding variational bayes. In ICLR 2014.
[8] Dinh, L., Sohl-Dickstein, J. and Bengio, S. Density estimation using Real NVP. In ICLR 2017.