Essay: VAE as a 1-step Diffusion Model
아래 글은 비공식적인 개인의 사견임을 밝힌다.
- Essay on VAE and its relationship to diffusion model
- Keyword: VAE, Diffusion Model, VDM, VLB
Introduction
DDPM[arXiv:2006.11239] 이후 Diffusion Model은 그 합성 품질에 힘입어 빠른 속도로 발전해 왔다.
DDPM과 VAE[arXiv:1312.6114]는 동일하게 Variational Lowerbounds(이하 VLB)를 통해 학습되지만, DDPM에서 더 High-fidelity의 이미지를 생성한다.
DDPM은 어떻게 VAE 보다 더 실제같은 이미지를 생성할 수 있었는가, 그에 대해 논의한다.
| VAE | DDPM | |
|---|---|---|
| Objective | VLB | VLB |
| Size of latent variable | Smaller than data dimension | Same with data dimension |
| Generation | Single forward pass | Multiple forward passe (T-steps) |
| Architecture | Autoencoder w/Bottleneck | U-Net w/Time-embedding |
Revisit: Variational Lowerbounds
VAE는 몇 가지 문제 상황을 가정한다.
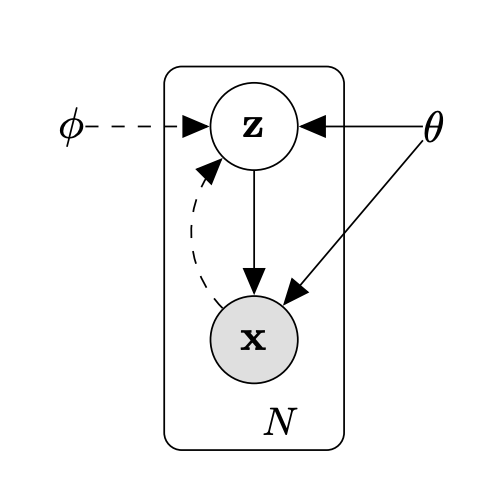
어떤 데이터셋 $X = \{x_i\}^N_{i=1}$는 Random variable $x$에서 i.i.d.로 샘플링되었다. 우리는 이 데이터가 관측되지 않은 random variable $z$에 어떤 random process를 취해 생성되었다 가정할 것이다.
$z$는 prior distribution $p(z)$에서 샘플링되고, $x$는 조건부 분포 $p(x|z;\theta)$에 의해 생성된다. (그리고 각 분포는 $z$와 $\theta$에 대해 미분가능하다 가정한다)
우리는 $p(z)$가 어떻게 생긴 분포인지 모르기 때문에, $p(x; \theta) = \int p(z)p(x|z; \theta)dz$의 marginalize가 불가능하다. (그렇기에 true posterior $p(z|x) = p(x|z)p(z)/(x)$ 역시 연산 불가능하다)
이에 대응하고자 VAE에서는 approximate posterior $q(z|x; \phi)$를 도입하여 $\phi$와 $\theta$를 동시에 업데이트할 수 있는 objective function $\mathcal L$을 제안하였다.
$$\log p(x;\theta) = \mathcal L(x; \theta, \phi) + D_{KL}(q(z|x;\phi) || p(z|x;\theta))$$ $$\mathcal L(x; \theta, \phi) = \mathbb E_{q(z|x; \phi)}\left[\log p(x|z; \theta)\right] - D_{KL}(q(z|x; \phi)||p(z))$$
$D_{KL}$은 0 이상 값을 가지므로 $\mathcal L(\theta, \phi; x)$는 log-likelihood의 하한이 되고, 이를 optimizing 하면 log-likelihood를 ascent 하는 것과 같은 효과를 볼 수 있다는 것이다.
DDPM 역시 Markov chain에 대한 variational lowerbound를 ascent 하는 방식으로 학습을 수행한다.
$x = x_0,\ z = x_T \sim \mathcal N(0, I)$의 T-step Diffusion Model을 가정할 때, variance schedule $\beta_1, …\beta_T$에 대해 forward process(noising) $q(x_t|x_{t-1})$와 reverse process(denoising) $p(x_{t-1}|x_t; \theta)$를 가정한다.
$$q(x_t|x_{t-1}) = \mathcal N(\sqrt{1 - \beta_t}x_{t-1}, \beta_t I), \ p(x_{t-1}|x_t; \theta) = \mathcal N(\mu_\theta(x_t; t), \Sigma_\theta(x_t, t))$$
이때 VLB는 동일하게 적용된다.
$$\log p(x; \theta) \ge \mathbb E_{q(x_0|x)}[\log p(x|x_0)] + \mathcal L_{T}(x; \theta) - D_{KL}(q(x_T|x)||p(z))$$ $$\mathcal L_{T}(x; \theta) = -\sum^T_{i=1}\mathbb E_{q(x_i|x)} D_{KL}\left[q(x_{i-1}|x_i, x)||p(x_{i-1}|x_i; \theta)\right]$$
학습 목적 함수는 사실상 같다고 봐야 한다.
Size of latent variables
VAE와 Diffusion Model의 차이로 떠오르는 것은 Bottleneck Architecture이다.
VAE는 latent variable의 dimension은 대개 데이터보다 작다. Diffusion은 markov chain 내의 state를 모두 latent variable로 바라보고, 각각의 latent variable은 데이터의 dimension과 크기가 같다.
작은 latent variable은 초기 GAN[arXiv:1406.2661] 기반의 모델에서도 공통으로 나타나는 특징이다.
이후 VAE와 GAN 모두, 데이터 차원과 같은 크기의 잠재 변수를 도입하여 성능 향상을 본 모델이 나온다. StyleGAN[arXiv:1812.04948]은 이미지의 stochastic detail을 생성하기 위해 $\mathbb R^{\mathrm{H\times W\times 1}}$의 single-channel noise를 더하였고, NVAE[arXiv:2007.03898]는 U-Net-like architecture를 도입하면서 residual signal을 latent variable로 모델링한다.
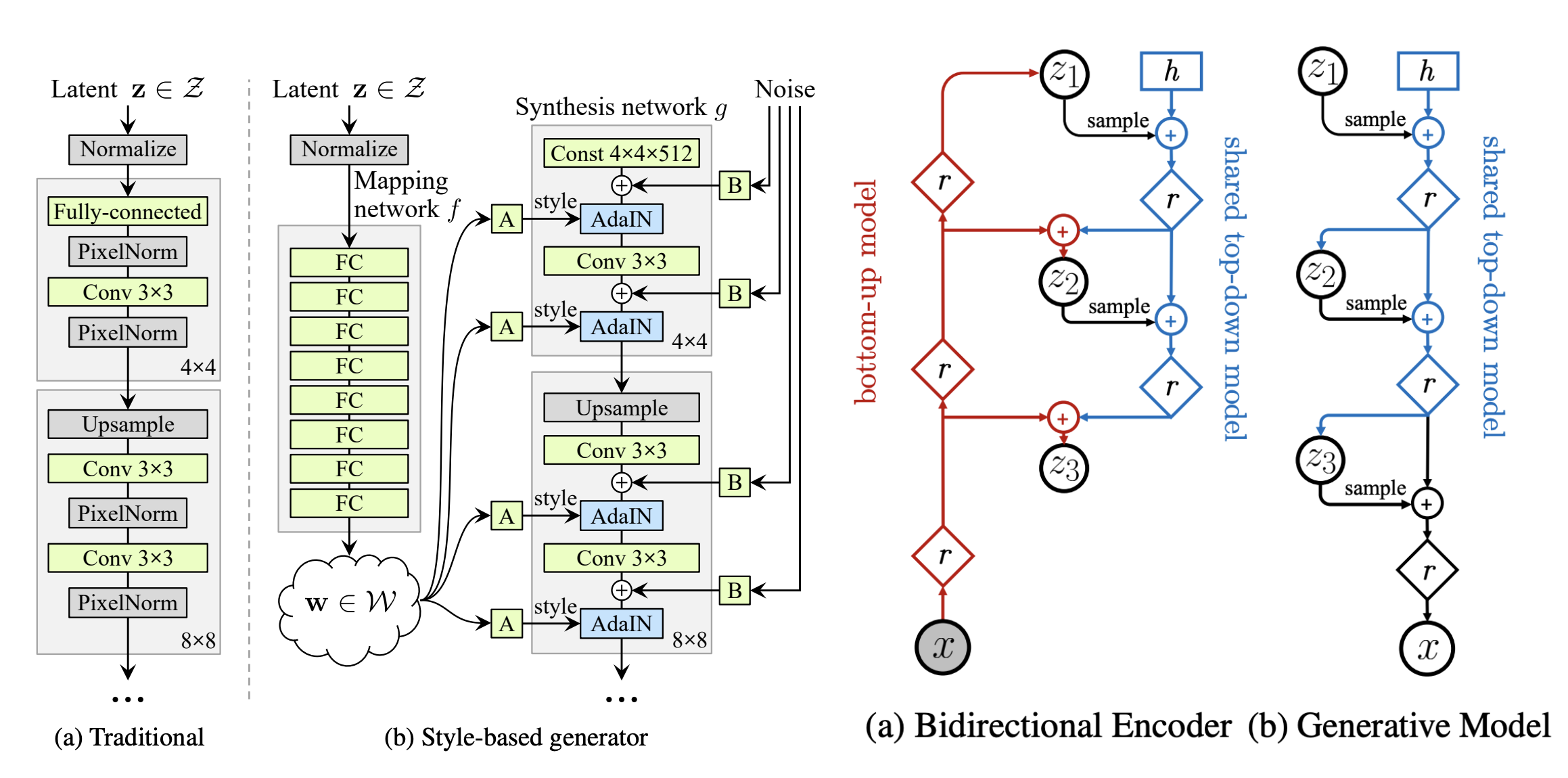
Left: Figure 1, Karras et al.(StyleGAN), 2018 / Right: Figure 2, Vahdat & Kautz(NVAE), 2020.
다만 둘 모두 이론적 근거를 제시하기보단 Ablation study를 통해 정량적, 정성적 개선 정도를 보인다.
이미지의 대략적인 형상과 배치 등 lower frequency의 정보는 작은 잠재 변수 공간에서 capture 할 수 있지만, Higher frequency의 정보를 capture 하기 위해서는 spatial information에 correlate 된 latent variable이 있어야 하지 않을까 싶은 정도이다.
VAE와 Diffusion의 합성 품질 차이는 latent variable의 크기에서 일부 기인했을 것으로 보인다.
VAE as a 1-step Diffusion Model
VAE가 이미지와 같은 크기의 잠재 변수를 취급하고, $z \mapsto x$의 매핑을 U-Net으로 모델링한다 가정하자. 동일하게 VLB를 통해 학습되고, 잠재 변수의 크기도 이미지의 차원과 같으며, U-Net을 디코더 백본으로 사용한다.
주어진 가정 아래 VAE는 $\beta_1 = 1$의 variance schedule을 가지는 T=1의 Single-step diffusion model로 볼 수 있다. T=1 이므로 timestep embedding을 배제하고 학습하여도 무방하며, timestep embdding을 포함하여 DDPM과 완전히 동일한 백본을 가정할 수도 있다.
$$q(x_1|x_0) = \mathcal N(\sqrt{1 - \beta_1}x_0, \beta_1 I) = \mathcal N(0, I) \Leftrightarrow p(z)$$ $$p(x_0|x_1) = \mathcal N(\mu_\theta(x_1), \Sigma_\theta(x_1)) \Leftrightarrow p(x|z; \theta)$$
1-step Diffusion model은 $x_0 = x, z = x_1 \sim \mathcal N(0, I)$을 상정하므로, 단순 이름 바꾸기를 통해 $p(x|z; \theta) = p(x_0|x_1; \theta)$를 얻을 수 있고, 이는 VAE의 generation process와 같다.
이 경우 Encoder의 위치에 관하여 고민해 볼 필요가 있다. VAE는 Encoder를 통해 posterior를 근사하지만, DDPM은 variance schedule을 통해 chain의 끝이 prior distribution에 충분히 가깝도록 설계한다.
$$\bar\alpha_t = \prod^t_{i=1}(1 - \beta_i) \Rightarrow q(x_t|x_0) = \mathcal N(\sqrt{\bar\alpha_t}x_0, (1 - \bar\alpha_t)I)$$
일반화를 위해 기존의 $q(x_t|x)$를 $q(x_t|x; \psi)$로 parametrize하고, $D_{KL}(q(x_T|x; \psi)||p(z))$ 역시 학습의 대상으로 삼자. 이 경우 $x_t = \sqrt{\bar\alpha_t}x + \sqrt{1 - \bar\alpha_t}\epsilon_\psi\ \mathrm{where}\ \epsilon_\psi \sim \mathcal N(\mu_\psi(x), \sigma^2_\psi(x))$로 모델링하여 VAE와 같이 $D_{KL}(\mathcal N(\mu_\psi(x), \Sigma_\psi(x))||p(z))$가 학습되도록 한다. ($\because x_T = 0\cdot x + 1\cdot\epsilon_\psi = \epsilon_\psi$)
$\mathcal L_T$의 $D_{KL}(q(x_{i-1}|x_i, x; \psi)||p(x_{i-1}|x_i; \theta))$는 $||x - x_\theta(\sqrt{\bar\alpha_t}x + \sqrt{1 - \bar\alpha_t}\epsilon_\psi; t)||^2_2$의 noise estimation loss 형태로 표현해 볼 수 있다. (w/reparametrization $\epsilon_\psi = \mu_\psi(x) + \sigma_\psi(x)\epsilon,\ \epsilon \sim \mathcal N(0, I)$)
이제 둘의 마지막 차이는 step의 수뿐이다.
More step is better
VDM[arXiv:2107.00630]에서는 step의 수가 많을수록 더 tight 한 VLB의 하한을 얻을 수 있다고 이야기한다.
variance preserving diffusion model에서의 SNR(signal-to-noise ratio)을 $\gamma^2_t = \frac{\bar\alpha_t}{1 - \bar\alpha_t}$로 표현하면, variance schedule $\beta_1, …\beta_{2T}$에 대해 목적함수 $\mathcal L_{2T}$는 다음으로 정리할 수 있다.
$$\mathcal L_{2T}(x; \theta) = -\frac{1}{2}\mathbb E_{\epsilon \sim \mathcal N(0, I)}\left[\sum^{2T}_ {t=1}(\gamma^2_{t-1} - \gamma^2_t)||x - x_\theta(x_t; t)||^2_2\right]$$
variance schedule을 유지한 채 step을 절반으로 줄이면 다음과 같이 표현할 수 있다.
$$\mathcal L_T(x; \theta) = -\frac{1}{2}\mathbb E_{\epsilon \sim\mathcal N(0, I)}\left[\sum^T_{t=1}(\gamma^2_{2(t-1)} - \gamma^2_{2t})||x - x_\theta(x_{2t}; 2t)||^2_2\right]$$
우리가 보이고 싶은 것은 $\mathcal L_{2T} - \mathcal L_T > 0$가 성립하여 $\mathcal L_{2T}$가 $\log p(x; \theta)$에 더 가까운 하한이라는 것이다.
$$\mathcal L_T(x; \theta) = -\frac{1}{2}\mathbb E_{\epsilon\sim\mathcal N(0, I)}\left[\sum^T_{t=1}(\gamma^2_{2(t-1)} - \gamma^2_{2t - 1} + \gamma^2_{2t - 1} - \gamma^2_{2t})||x - x_\theta(x_{2t}; 2t)||^2_2\right]$$ $$\begin{align*}\mathcal L_{2T}(x; \theta) = -\frac{1}{2}\mathbb E_{\epsilon\sim\mathcal N(0, I)}&\left[\sum^T_{t=1}(\gamma^2_{2t - 1} - \gamma^2_{2t})||x - x_\theta(x_{2t}; 2t)||^2_2\right. \\&+ \left.\sum^T_{t=1}(\gamma^2_{2(t-1)} - \gamma^2_{2t-1})||x - x_\theta(x_{2t-1}; 2t-1)||^2_2 \right]\end{align*}$$ $$\mathcal L_{2T}(x; \theta) - \mathcal L_{T}(x; \theta) = -\frac{1}{2}\mathbb E_{\epsilon\sim\mathcal N(0, I)}\left[\sum^T_{t=1} (\gamma^2_{2(t-1)} - \gamma^2_{2t-1})(||x - x_\theta(x_{2t-1}; 2t-1)||^2_2 - ||x - x_\theta(x_{2t}; 2t)||^2_2) \right]$$
variance schedule에서 $\gamma_t$는 대개 감소함수로 설정되므로, $\gamma^2_{2(t-1)} - \gamma^2_{2t-1}$은 양수이다.
$||x - x_\theta(x_{2t-1}; 2t-1)||^2_2 - ||x - x_\theta(x_{2t}; 2t)||^2_2$는 2t-1번째 스텝에서 추정한 데이터와 2t번째 스텝에서 추정한 데이터 각각의 MSE를 다룬다. 잘 학습된 네트워크 입장에서는 상대적으로 SNR이 높은 2t-1번째 스텝에서 데이터를 추정하기 더 쉬울 것이고, 그렇기에 MSE 값은 상대적으로 낮게 측정될 것이다. 결국 MSE의 차는 음수로 떨어진다.
가장 앞단의 부호를 포함하면 $\mathcal L_{2T} - \mathcal L_T$는 양수가 되고, $\mathcal L_{2T}$가 tighter lower bound가 된다.
VAE를 1-step Diffusion model로 볼 경우, 1천 스텝 정도를 다루는 Diffusion model에 대비하여 NLL(Negative log-likelihood)이 높게 측정될 가능성이 높다. 물론 NLL이 낮다고 visual quality가 좋은 것은 아니나, 그 가능성 측면에서는 유의미하게 해석할 수 있는 지표일 것이다.
How about a 1,000-step VAE ?
반대로 VAE를 Diffusion model처럼 1천번 forward pass 하여 성능 개선이 가능할지도 고민해 볼 법하다. 네트워크로부터 데이터 포인트를 생성하고, forward process(noising)을 거쳐 다시 네트워크에 통과시키는 것을 가정하자.
$$\tilde x_t = \mathrm{Decoder}(x_t; \theta),\ x_{t-1} = \sqrt{\bar\alpha_{t-1}}\tilde x_t + \sqrt{1 - \bar\alpha_{t-1}}\epsilon\ \mathrm{where}\ \epsilon \sim \mathcal N(0, I),\ t=1000,…,0$$
Diffusion model은 $D_{KL}(q(x_{i-1}|x_i, x)||p(x_{i-1}|x_i; \theta))$을 통해 하나의 데이터를 두고, noised sample에서 noise를 줄여가는 방향으로 학습한다. 충분히 작은 noise를 데이터에 더하여 t=1의 네트워크에 통과시킬 경우, 네트워크의 출력물로 원본 데이터가 나올 것이라 기대할 수 있다.
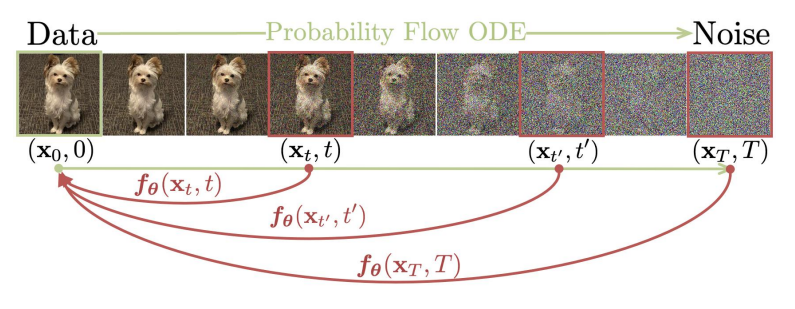
Generation trajectory (Figure 1, Song et al., 2023)
반면 VAE는 $0.99999\times x + 0.00001\times\epsilon$을 입력으로 하여도 $x$가 나올 것이라 기대할 수 없다. VAE는 학습 중에 posterior를 prior에 가까워지게 할 뿐이다. 보수적으로는 noised sample 역시 prior에서 샘플링하였다 가정해야 하고, 1천번의 수행 과정에서 1천개의 서로 다른 이미지가 나올 수도 있다.
이를 대응하기 위해서는 noised sample에 대해 원본 샘플이 나오도록 학습해야 하고, Consistency model[arXiv:2303.01469]과도 관련이 있어 보인다.
$$\mathcal L(\theta, \theta^-) \leftarrow \lambda(t_n)d(f_\theta(x + t_{n+1}z, t_{n+1}), f_{\theta^-}(x + t_nz, t_n))$$
Wrap up
Diffusion의 합성 품질은 latent variable의 크기와 sampling step의 수에 기인했을 것으로 보인다. 또한 VAE를 1-step Diffusion으로 해석할 수도 있으나, 1000-step VAE로는 성능 향상을 기대할 수 없다는 것도 확인하였다.
근래에는 datum point를 prior distribution으로 transport 하는 trajectory에 관하여도 연구가 많은 듯 보인다. 이에 관하여도 연관하여 고민하면 좋을 듯하다.
References
- Consistency Models, Song et al., 2023. [arXiv:2303.01469]
- VDM: Variational Diffusion Models, Kingma et al., 2021. [arXiv:2107.00630]
- NVAE: A Deep Hierarchical Variational Autoencoder, Vahdat & Kautz, 2020. [arXiv:2007.03898]
- DDPM: Denoising Diffusion Probabilistic Models, Ho et al., 2020. [arXiv:2006.11239]
- StyleGAN: A Style-Based Generator Architecture for Generative Adversarial Networks, Karras et al., 2018. [arXiv:1812.04948]
- GAN: Generative Adversarial Networks, Goodfellow et al., 2014. [arXiv:1406.2661]
- VAE: Autoencoding Variational Bayes, Kingma & Welling, 2013. [arXiv:1312.6114]